Problem 1: actions with unknown consequences

Updates are in red.

    In deterministic state space models, we assume that the agent's actions deterministically lead to a successor state which is observed. MDPs allow us to handle the situation where actions result in a known distribution over possible successor states; the successor state is unknown before taking the action, but observed after taking the action. In this problem, we'll consider the case where we don't have a distribution over successor states, and we might not even observe the successor state after taking an action.

    Consider a state space model with starting state $s_\text{start}$ and goal state $s_\text{goal}$. For each state $s$ and possible action $a \in \text{Actions}(s)$, instead of a successor function $\text{Succ}(s, a)$ that returns the resulting state deterministically, we have $\text{SuccSet}(s, a)$, which returns a set of possible states that the agent could end up in. Each successor in $\text{SuccSet}(s, a)$ has positive probability. Importantly, before you take an action, you will not know which of the possible states you will end up in.

    To make things simple, assume that all actions are possible from all states with the same cost. Define two scenarios:

    Define two goals: In the following, you will construct state space models (which can be either deterministic state space models, MDPs, or general games). You should pick the simplest model that is sufficient to solve the problem.

    As an example, consider the following model. Let there be two actions, $\{Forward, Forward2\}$. $\text{SuccSet}(s_\text{start}, Forward) = \{B,C\}$, $\text{SuccSet}(s_\text{start}, Forward2) = \{C,D\}$, $\text{SuccSet}(B, Forward) = \text{SuccSet}(C, Forward) = \{s_\text{goal}\}$. All unmentioned state/action pairs return the empty set.

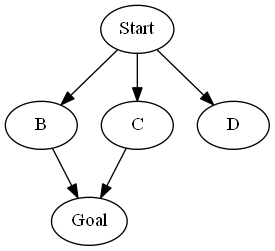
    Under Scenario 2, the sequence of actions, $[Forward, Forward]$ will achieve Goal 1 and Goal 2, whereas $[Forward2, Forward]$ will only achieve Goal 2.

  1. [2 points] Construct a state space model to achieve Goal 1 under Scenario 1.
  2. [2 points] Construct a state space model to achieve Goal 2 under Scenario 1.
  3. [2 points] Construct a state space model to achieve Goal 1 under Scenario 2.
  4. [2 points] Construct a state space model to achieve Goal 2 under Scenario 2.
  5. [2 points] Let $c_{i,g}$ be the cost of the minimum cost path returned for Scenario $i$ and Goal $g$. Specify all relationships between the values $c_{i,g}$ which are guaranteed to hold (e.g., one quantity is always at most another quantity).
  6. [2 points] Suppose we're in Scenario 2. For Goal 1, describe a consistent A* heuristic based on the solution of Goal 2.

Problem 2: resource allocation

    People love iBuckets. Each quarter, people demand a certain number of iBuckets ($d_i$ in quarter $i$). If there ever comes a time when in the previous quarter, no one wants iBuckets (if $d_{i-1} = 0$), then no one will want iBuckets now ($d_i = 0$). Otherwise, the demand $d_i$ is either exactly one more than the previous quarter (with probability $\alpha_+$), the same (with probability $\alpha_=$) or exactly one fewer (with probability $\alpha_-$) than the previous quarter's demand $d_{i-1}$. Initially, the demand is $d_0 = 100$.

    Fortunately, you have a company that has a monopoly on iBuckets. You have a factory with some number of iMachines $m_i$ at quarter $i$. You can make each iMachine produce either zero or one iBucket per quarter. In addition, each quarter, you can buy up to $K$ new iMachines to add to the ones you already have or remove up to $K$ old iMachines, and this will determine $m_{i+1}$ for quarter $i+1$. Initially, you have no iMachines ($m_i = 0$).

    Each new iMachine costs $b_i$ dollars to buy (one time cost), $k_i$ dollars to maintain per quarter, and $r_i$ dollars to remove (one time cost).

    Each new iMachine costs $b$ dollars to buy (one time cost), $k$ dollars to maintain per quarter, and $r$ dollars to remove (one time cost).

    Each quarter, you choose to produce $s_i$ iBuckets (which can be no more than your production capacity $m_i$). Each iBucket costs $c_i$ dollars to make and sells for $p_i$ dollars. Each iBucket costs $c$ dollars to make and sells for $p$ dollars. Of course, you can't sell more than the demand $d_i$ or more than you actually produce $s_i$. For simplicity, assume $p_i > c_i$, and you cannot store unsold iBuckets for the next quarter. For simplicity, assume $p > c$, and you cannot store unsold iBuckets for the next quarter.

    Your profit each quarter $u_i$ is the revenue from sales minus total operating costs. Your goal is to maximize the total profit $\sum_{i=0}^\infty u_i$.

    If $d_i = d_\max = 200$, then $d_{i+1}$ stays the same or decreases with equal probability. This is purely a technicality to make the state space finite (we don't care that you include this in your answer).

    [5 points] Formulate this problem as a Markov decision process. What are the states, actions, transition distribution, reward function, initial state, and terminal state(s) (if there are any)?

Problem 3: optimal policies in MDPs

  1. [2 points] Many MDPs in practice do not have cycles (e.g., Blackjack, because cards can only be dealt, not taken back), there is always forward progress. Recall that in deterministic state space models, acyclicity allowed us to use the more efficient DAG search instead of Bellman-Ford. Suppose the state space graph of an MDP is acyclic. Explain how to adapt DAG search to compute the optimal value $V(s)$. You should be specific but brief (do not give pseudocode).
  2. [2 points] Suppose the state space graph of an MDP does not have cycles. Prove that value iteration will converge in a finite number of iterations. Hint: use induction.
  3. [2 points] Suppose we initialize value iteration with $V^\pi$ rather than 0 for some arbitrary $\pi$. Will this always converge faster (as measured by the distance of your estimated values to the true values)? Either prove or give a small concrete counterexample.
  4. [1 point] Let $A(s)$ be the expected utility from alternating between policies $\pi$ and $\sigma$, starting with $\pi$. Write down a recurrence for $A(s)$. You might find it useful to define an intermediate function.

Problem 4: modified reward functions

Given an MDP with a reward function $\text{Reward}(s, a)$, we can compute the optimal policy $\pi_\text{opt}(s)$. For what values of $c$ (you must specify the exact set) do the following modified reward functions yield the same optimal policy? In each case, prove or give a simple counterexample.
  1. [1 point] $c \cdot \text{Reward}(s, a)$
  2. [1 point] $\text{Reward}(s, a) + c$,
  3. [1 point] $\text{Reward}(s, a)^c$

Problem 5: traveling with traffic

    Let $C$ be a set of cities which are joined by a set of roads $R$ ($(i,j) \in R$ means you can take a road from $i$ to $j$), and it takes $t_{i,j}$ time to traverse the road. However, the traffic can add additional delays. Specifically, if you're in city $i$ and try to go to city $j$, you'll succeed with probability $1-\alpha_i$ and fail with probability $\alpha_i$, in which case you stay in city $i$; the success does not depend on previous trials. If you fail, it takes $u_{ij} > 0$ time, and if you succeed, it takes $v_{ij} > u_{ij}$ time. Your goal is to go from city $c_1 \in C$ to city $c_2 \in C$ in the minimum expected time (your utility is total commute time).
  1. [3 points] Formulate this problem as an MDP (what are the states, actions, rewards, transitions?).
  2. [2 points] Construct a deterministic state space model so that the optimal policy in the MDP is the same as the minimum cost path in the deterministic state space model. and the expected utility of that policy is also the same. Note that for this to make sense, the MDP and the deterministic state space model must have the same set of states and actions.

Problem 6: a multi-player game

Consider an $n$-person game. On person $i$'s turn, he or she gets one point. Then he chooses another person $j \neq i$, and it is person $j$'s turn. The game ends when someone gets 10 points; that person wins. Consider the following three policies:
The agent (you) gets to go first. Also, note that there might be many optimal policies for each player; break ties by assuming each player (if playing optimally) will always return the policy which chooses uniformly over actions with the same maximum expected utility. For parts b and c, we're only looking for a short intuitive answer (the point is to just to get you thinking about policies in multiplayer games).
  1. [3 points] Formulate this problem as a game (what are the states, actions, players, successor function, rewards, starting state, and terminal states?).
  2. [1 point] Assume all the other $n-1$ people are playing optimally. Which of the three policies listed above are rational? No proof is necessary - just give your intuition.
  3. [1 point] Suppose at least one of the other people are not playing optimally. Which of the three policies listed above are rational? No proof is necessary - just give your intuition.