Smoothed state estimates under abrupt changes using sum-of-norms regularization
Automatica, 48:595-605, February 2012.
Awarded Automatica Best Paper Prize at 2014 IFAC World Congress.
The presence of abrupt changes, such as impulsive and load disturbances,
commonly occur in applications, but make the state estimation problem
considerably more difficult than in the standard setting with Gaussian process
disturbance. Abrupt changes often introduce a jump in the state, and the
problem is therefore readily and often treated by change detection techniques.
In this paper, we take a different approach. The state smoothing problem for
linear state space models is here formulated as a constrained least-squares
problem with sum-of-norms regularization, a generalization of
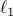 -regularization. This novel formulation can be seen as a convex relaxation of
the well known generalized likelihood ratio method by Willsky and Jones.
Another nice property of the suggested formulation is that it only has one
tuning parameter, the regularization constant which is used to trade off fit
and the number of jumps. Good practical choices of this parameter along with an
extension to nonlinear state space models are given.
-regularization. This novel formulation can be seen as a convex relaxation of
the well known generalized likelihood ratio method by Willsky and Jones.
Another nice property of the suggested formulation is that it only has one
tuning parameter, the regularization constant which is used to trade off fit
and the number of jumps. Good practical choices of this parameter along with an
extension to nonlinear state space models are given.