Contents
function h = finance
Problem data
s = RandStream.create('mt19937ar','seed',0);
RandStream.setDefaultStream(s);
n = 20;
T = 15;
F = randn(n);
S = F*F';
d = abs(randn(n,1));
gam = 1;
mu = randn(n,1);
kappa = unifrnd(0,3,n,1);
f = @(u) -mu'*u + (gam/2)*quad_form(u,S);
g = @(u) kappa'*pow_pos(abs(u), 1.5);
CVX (static)
tic
cvx_begin quiet
variable xs(n)
minimize(f(xs))
subject to
sum(xs) <= 1
xs >= 0
cvx_end
h.xs = xs;
toc
Elapsed time is 0.095368 seconds.
CVX (dynamic)
tic
cvx_begin quiet
cvx_solver sdpt3
variable x(n,T)
expression obj
obj = f(x(:,1));
for t = 2:T
obj = obj + f(x(:,t)) + g(x(:,t) - x(:,t-1));
end
minimize(obj)
subject to
sum(x) <= 1
x >= 0
x(:,1) == 0;
x(:,T) == 0;
cvx_end
toc
p_cvx = cvx_optval;
Elapsed time is 2.230762 seconds.
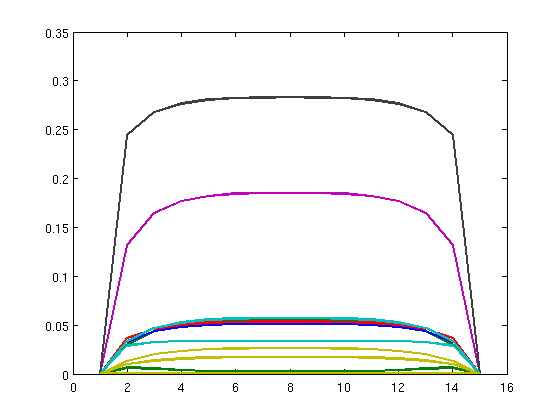
Plots
figure(1);
plot(x', 'LineWidth', 2);
xlim([0 T+1]);
print -depsc fin_asset_holdings.eps;
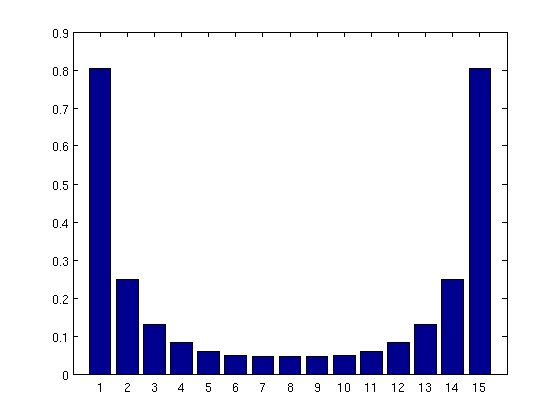
figure(2);
bar(norms(x - repmat(xs,1,T), 1));
xlim([0 T+1]);
print -depsc fin_deviation.eps;
ADMM
MAX_ITER = 100;
ABSTOL = 1e-4;
RELTOL = 1e-2;
lambda = 1;
x = zeros(n,T);
z = zeros(n,T);
u = zeros(n,T);
fprintf('\n\n%3s\t%10s\t%10s\t%10s\t%10s\n', 'iter', ...
'r norm', 'eps pri', 's norm', 'eps dual');
for k = 1:MAX_ITER
for t = 2:T-1
cvx_begin quiet
variable xt(n)
minimize(f(xt) + (1/(2*lambda))*sum_square(xt - z(:,t) + u(:,t)))
subject to
xt >= 0
sum(xt) <= 1
cvx_end
x(:,t) = xt;
end
zold = z;
cvx_begin quiet
cvx_solver sdpt3
variable z(n,T)
obj = 0;
for t = 2:T
obj = obj + g(z(:,t)-z(:,t-1));
end
minimize(obj + (1/(2*lambda))*square_pos(norm(z - x - u,'fro')))
subject to
z(:,1) == 0;
cvx_end
u = u + x - z;
h.r_norm(k) = norm(x - z,'fro');
h.s_norm(k) = norm(-(z - zold)./lambda,'fro');
h.eps_pri(k) = sqrt(n*T)*ABSTOL + RELTOL*max(norm(x,'fro'), norm(-z,'fro'));
h.eps_dual(k) = sqrt(n*T)*ABSTOL + RELTOL*norm(u./lambda,'fro');
h.objval(k) = f(x(:,1));
for t = 2:T
h.objval(k) = h.objval(k) + f(x(:,t)) + g(x(:,t) - x(:,t-1));
end
fprintf('%3d\t%10.4f\t%10.4f\t%10.4f\t%10.4f\n', k, ...
h.r_norm(k), h.eps_pri(k), h.s_norm(k), h.eps_dual(k));
if h.r_norm(k) < h.eps_pri(k) && h.s_norm(k) < h.eps_dual(k)
break;
end
end
h.admm_iter = k;
h.x_admm = x;
h.mu = mu;
iter r norm eps pri s norm eps dual
1 0.2739 0.0122 0.9409 0.0045
2 0.2108 0.0138 0.2525 0.0065
3 0.1744 0.0142 0.0813 0.0081
4 0.1455 0.0143 0.0398 0.0094
5 0.1223 0.0143 0.0273 0.0105
6 0.1039 0.0142 0.0210 0.0114
7 0.0892 0.0142 0.0167 0.0122
8 0.0775 0.0142 0.0134 0.0129
9 0.0680 0.0141 0.0108 0.0135
10 0.0604 0.0141 0.0088 0.0140
11 0.0541 0.0141 0.0072 0.0144
12 0.0487 0.0141 0.0060 0.0148
13 0.0442 0.0141 0.0051 0.0151
14 0.0402 0.0141 0.0043 0.0155
15 0.0367 0.0141 0.0037 0.0157
16 0.0336 0.0141 0.0032 0.0160
17 0.0309 0.0141 0.0028 0.0162
18 0.0284 0.0141 0.0025 0.0164
19 0.0261 0.0140 0.0022 0.0166
20 0.0241 0.0140 0.0020 0.0168
21 0.0222 0.0140 0.0018 0.0169
22 0.0205 0.0140 0.0016 0.0171
23 0.0190 0.0140 0.0015 0.0172
24 0.0176 0.0140 0.0013 0.0173
25 0.0163 0.0140 0.0012 0.0174
26 0.0151 0.0140 0.0011 0.0175
27 0.0140 0.0140 0.0010 0.0176
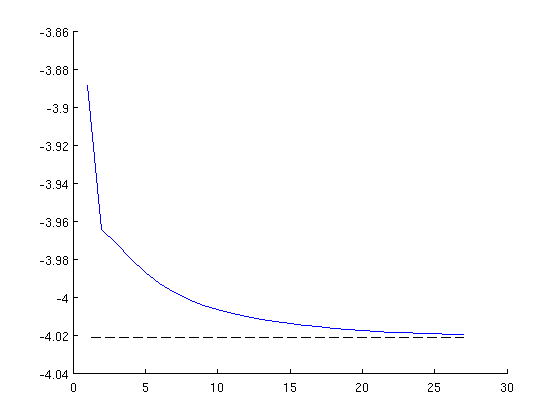
Plots
figure(3);
hold on;
plot(h.objval');
plot(repmat(p_cvx, 1, k), 'k--');
print -depsc fin_optval.eps;