Optimal Current Waveforms for Brushless Permanent Magnet Motors

International Journal of Control, 88(7):1389-1399, 2015.

• Final paper

In this paper we give energy-optimal excitation current waveforms for a permanent magnet synchronous motor that result in a desired average torque. Our formulation generalizes previous work by including a general back-EMF waveform, voltage and current limits, an arbitrary phase winding connection, a simple eddy current loss model, and a trade-off between power loss and torque ripple. Determining the optimal current waveforms requires solving a small convex optimization problem. 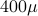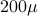We give a fast algorithm to find the optimal current waveforms in around s; changes in required torque can be handled in around s even on low-cost processors. We show that for an ideal motor with sinusoidal back-EMF, the optimal current waveforms increase efficiency by several percent in the constant power region. We also show that, for our model parameters, a sinusoidal back-EMF gives no performance benefit over a trapezoidal back-EMF, even in the constant power region, provided the optimal current waveforms are used. Another advantage of on-line optimization is the ability to adapt in real time to changes in the model or requirements, such as changes in resistance as winding temperature varies, or even gross changes like the failure of one winding.