A Semidefinite Programming Method for Integer Convex Quadratic Minimization
J. Park and S. Boyd
Optimization Letters, 12(3):499–518, May 2018.
We consider the NP-hard problem of minimizing a convex quadratic function over
the integer lattice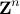 
. We present a simple semidefinite
programming (SDP) relaxation for obtaining a nontrivial lower bound on the
optimal value of the problem. By interpreting the solution to the SDP
relaxation probabilistically, we obtain a randomized algorithm for finding
good suboptimal solutions, and thus an upper bound on the optimal value. The
effectiveness of the method is shown for numerical problem instances of
various sizes.