Contents
Generate problem data
randn('state', 0);
rand('state', 0);
n = 100;
P = rand(n);
P = P + P';
[V D] = eig(P);
P = V*diag(1+rand(n,1))*V';
q = randn(n,1);
r = randn(1);
l = randn(n,1);
u = randn(n,1);
lb = min(l,u);
ub = max(l,u);
Solve problem
[x history] = quadprog(P, q, r, lb, ub, 1.0, 1.0);
iter r norm eps pri s norm eps dual objective
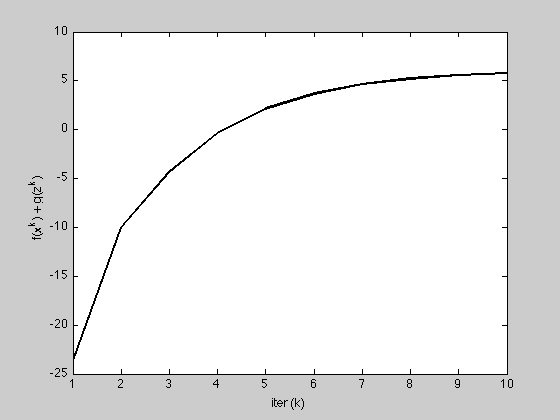
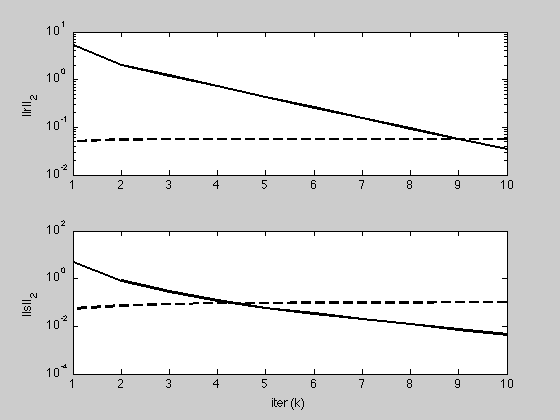
1 5.4585 0.0508 4.9772 0.0556 -23.62
2 2.0050 0.0546 0.8151 0.0734 -10.06
3 1.2096 0.0558 0.2823 0.0845 -4.36
4 0.7197 0.0562 0.1188 0.0912 -0.39
5 0.4287 0.0564 0.0578 0.0952 2.14
6 0.2564 0.0564 0.0331 0.0976 3.70
7 0.1541 0.0564 0.0199 0.0990 4.64
8 0.0931 0.0564 0.0120 0.0999 5.21
9 0.0566 0.0564 0.0073 0.1004 5.55
10 0.0345 0.0564 0.0044 0.1007 5.75
Elapsed time is 0.019595 seconds.
Reporting
K = length(history.objval);
h = figure;
plot(1:K, history.objval, 'k', 'MarkerSize', 10, 'LineWidth', 2);
ylabel('f(x^k) + g(z^k)'); xlabel('iter (k)');
g = figure;
subplot(2,1,1);
semilogy(1:K, max(1e-8, history.r_norm), 'k', ...
1:K, history.eps_pri, 'k--', 'LineWidth', 2);
ylabel('||r||_2');
subplot(2,1,2);
semilogy(1:K, max(1e-8, history.s_norm), 'k', ...
1:K, history.eps_dual, 'k--', 'LineWidth', 2);
ylabel('||s||_2'); xlabel('iter (k)');