Stanford University
MS&E 217, Combinatorial Optimization

Autumn 2003-04

 

Home | Handouts | General Information

 

Announcements

 

(Archive)

 
  • (12/1) Extended office hours (2-4) on M Dec 1, W Dec 3, and from 1:00-3:00 pm on M Dec 8.
  • (12/1) Discussion section on Dec 5th – will discuss problems from the set below. If you have any preferences from within these (or from outside), let me know by Thu morning.
  • (12/1) Handout 13 is now online: Practice problems for the final.
  • (11/30) Online poll results: In class final.

Class Information

 

Location

 

Redwood G19

Time

 

MW 9:30--10:45

Discussion Section

 

F 9:30--10:45

Instructor

 

Ashish Goel (ashishg@stanford.edu)
Office: Terman 311
Phone: (650) 724-1463
Office hours: MW 2:00-3:00 in Terman 311

Syllabus, Evaluation, homeworks

 

Please see the general information page.

Discussion sessions schedule

 

Date

 

Topics

26 Sept

 

No session

3 Oct

 

Data structures Linear Programming

10 Oct

 

Linear programming Data structures

17 Oct

 

Make-up class

24 Oct

 

Matroids (MS&E 317 only)

31 Oct

 

Problem solving (practice for the midterm)


Optional Excercises

 

1.1

 

Consider the following algorithm:

Given: a positive integer n.
Goal: Find a factor of n.

Algorithm: Factor(n)

 

for i <-- 2 to sqrt(n)
      if  (i divides n)
           return i
      endif
endfor
return "prime"


Question: Is this an efficient algorithm?

 

Answer: No. The definition in class said that an algorithm is efficient if its running time is polynomial in the input size. In this case, the input is n. But to write down the integer n, we need roughly log n bits. So the “size” of the input is only X =  log n. The running time of the algorithm is sqrt(n), which is polynomial in n, but NOT in the input size X; it isO( 2X/2) which is exponential in the input size.

 

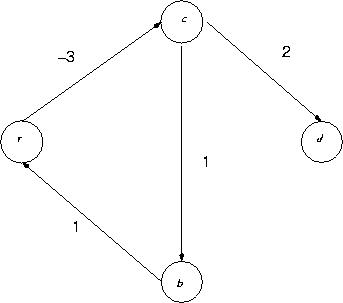
2.1

 

Show that there exists an infinite series of relaxations for the following graph:
Graph for problem 2.1

 

Answer: The pattern of relaxations ab,bc,ca can be repeated infinitely often.

 

3.1

 

Find a simple modification to the Bellman-Ford algorithm (as discussed in class) that enables it to determine if a negative cost cycle exists.

Answer: Run the algorithm for n iterations as opposed to n-1; if any potential changes in the n-th iteration, then there exists a negative cycle.

 

5.1

 

Show that for the fractional knap-sack problem, it is sufficient to examine finitely many possible allocations.

Answer: At most one item is picked fractionally, and can be picked in n different ways. We can pick up any subset of the remaining n-1 items, which makes a total of at most n2n-1 possible choices.

 

6.1

 

What impact do –ve weight edges have in the minimum spanning tree problem? Is there a simple pre-processing step that gets rid of –ve weight edges?

Answer: Minimum weight edges have no impact on the mst problem. Also, we can add a large positive value to each edge-weight to make sure all edge weights are non-negative.

 

16.1

 

Prove that in the case when we are given both lower bounds le and upper bounds ue on the flow xe through an edge, we can assume le ≠ -∞.

Hint: Read page 98 on the text and exercise 4.1.

 

17.1

 

Show that there exists a set of preferences such that the stable mrriage algorithm of Gale and Shapley requires Omega(n2) days to complete.

 

18.1

 

Suppose G is a bipartite graph and M is a matching in G. Use max-flow/min-cut techniques to prove that there is no M-augmenting path iff M is a maximum matching.

 

Announcements Archive