Reduced-order models (ROMs) are usually thought of as computationally inexpensive mathematical representations that offer
the potential for near real-time analysis. While most ROMs can operate in near real-time, their construction can however
be computationally expensive as it requires accumulating a large number of system responses to input excitations.
Furthermore, ROMs usually lack robustness with respect to parameter changes and therefore must often be rebuilt for each
parameter variation.
Together, these two issues underline the need for a fast and robust method for adapting pre-computed ROMs to new sets of
physical or modeling parameters. However, ROMs and their corresponding reduced-order bases (ROBs) are quantities that
typically belong to nonlinear, matrix manifolds. As such, classical interpolation methods fail, as they are not able to
enforce the constraints characterizing those manifolds. The first part of the project consists of designing a suitable
interpolation method enforcing those constraints. A schematic representation of the algorithm is shown below: it relies on
identifying the correct manifold for the given application, constructing the appropriate logarithm mapping to move the
interpolation data to a tangent space to this manifold where a standard multivariate interpolation algorithm can be applied,
and constructing the appropriate exponential mapping to bring back the computed result to the manifold of interest.
|
An approach based on database of reduced-order fluid bases and reduced-order structural models coupled with this method of
interpolation on a manifold, has been recently shown to greatly reduce computational cost for aeroelastic predictions of a
full F16 Block 40 aircraft while retaining good accuracy. The proposed method enables test operation calls for new,
``last minute'' flight configurations and thus paves the way for on-line, routine usage of reduced-order modeling including
during flight testing. Currently, its full potential is limited by the need to recompute a steady state flow for each desired
set of flight conditions not represented in the database.
Current work focuses on removing this limitation by developing a method for interpolating directly the fluid ROMs instead
of the underlying fluid ROBs.
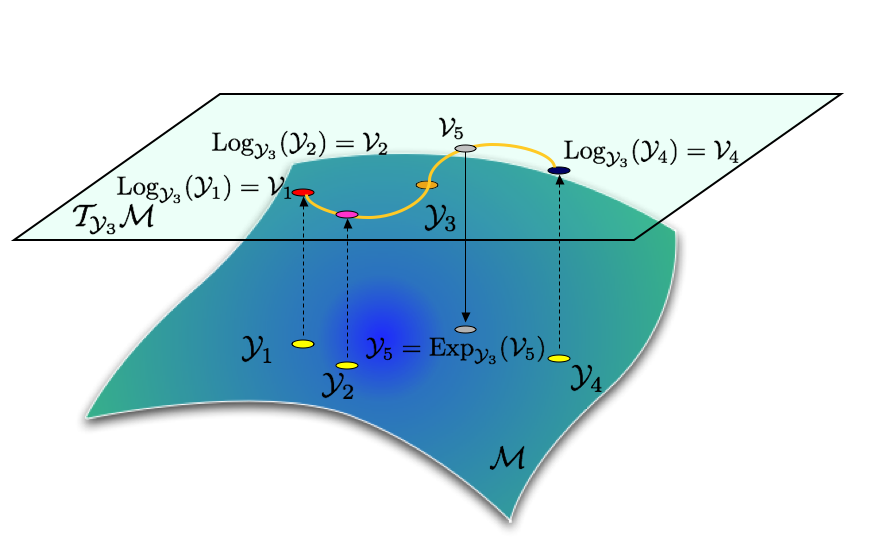 |
| Figure 2: Interpolation on a matrix manifold. |
|

