Optimization techniques have become indispensable tools for myriad
applications, including design, structural damage detection, and
inverse problems. However, executing an optimization procedure can be
prohibitively expensive, as it incurs repeated analyses of a high-
fidelity (e.g. detailed finite element or finite volume) model of the
physical system in different configurations (figure 1).
To this end, this project is focused on developing a framework for
decreasing the cost of such repeated analyses while guaranteeing the
satisfaction of any accuracy requirement. This framework is driven by
two principles: exploit data from previous analyses as much as
possible during future analyses, and accelerate convergence of new
analyses using this data. The first principle is achieved by computing
a proper orthogonal decomposition (POD) basis that optimally
represents the state and sensitivity vectors computed at previous
optimization steps.
|
To meet requirements of the second principle, a
fast POD-based iterative solver is used. This solver employs the POD
basis to accelerate convergence of the iterative solver used to
evaluate the high-fidelity model. This approach guarantees cost
savings because the POD basis can only accelerate convergence.
Furthermore, the satisfaction of accuracy requirements is promised
because the iterative method can continue to iterate until these
requirements are met. When this framework is used, the high-fidelity
model becomes less computationally expensive to evaluate as the
optimization progresses (figure 2). This is due to the increase in
size of the dataset and therefore continual improvement in quality of
the POD basis.
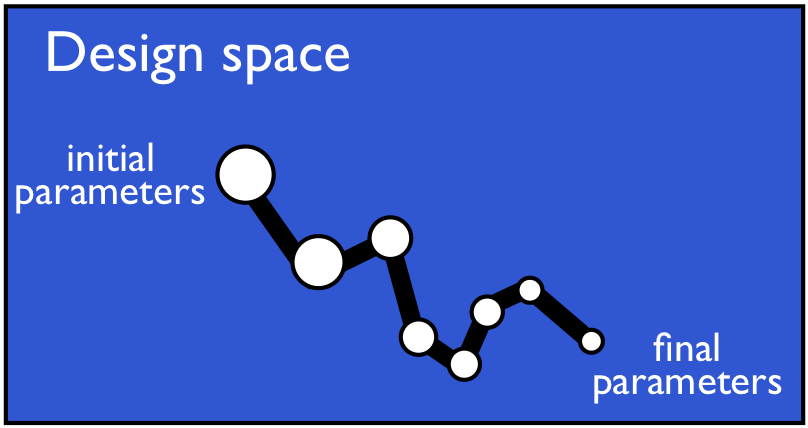 |
| Figure 2: Framework as applied to a gradient-based optimization
problem. Circle size is proportional to computational cost, and the black lines represent the optimization trajectory. |
|

