Woven materials have been used in body armor since ancient times. The invention of Kevlar, developed in 1965 at DuPont,
helped make structural fabrics a popular choice for modern personnel protection. Kevlar has been used in police body armor,
in the private section, and, starting in the 1980s, as part of the US army’s PASGT helmet and vest. While perhaps the most
well known example, Kevlar is just one of many such structural fabrics (others include Spectra, Twaron, and Zylon) that are
popular due to their flexibility and high strength-to-weight ratio. Beyond protecting personnel as body armor, these
materials have been integrated into vehicles and structures. The airline industry has employed ballistic fabrics like Kevlar
in the design of commercial aircraft. Ever since the crash of flight 232 in 1989 just outside of Sioux City Iowa, aircraft and
engine manufacturers have been concerned with rotorburst phenomena. Jet engine manufacturers (such as GE and Rolls Royce)
have been using ballistic fabrics to surround the engine turbines in an effort to impede fragments of the rotor that may break
off. However, large-scale experimental testing can be far too expensive and time consuming to be a feasible design tool.
Experimental tests of a jet engine’s ability to contain a rotor fragment costs on the order of ten million dollars. As the uses
for these materials continue to multiply and new fabrics are introduced, fast accurate computational models become increasingly
important.
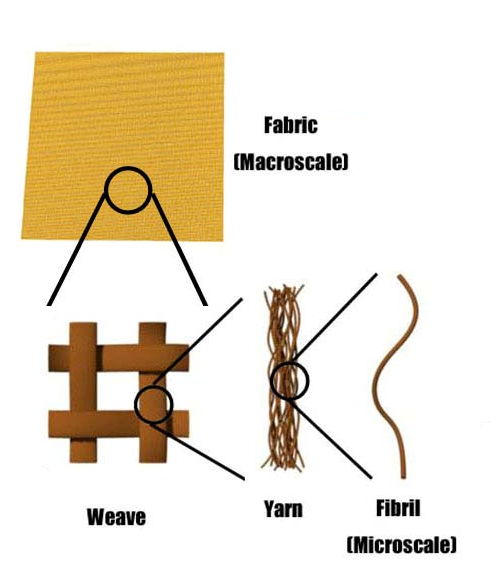
In order to model the impact of a projectile into these fabrics, figure 1, a multi-scale approach is taken that exploits the
multi-scale nature of the material. At the macro-scale, the weave pattern of the fabric sheet is easily discernible. This
weave is made up of thousands of yarn and each of these yarn are woven from hundreds of micro-scale fibrils, figure 2. Our
approach begins at the micro-scale with the fibrils and creates a model to predict the yarn response. This yarn model is then
placed into a numerical weave in order to capture the behavior of the macro-scale fabric sheet. This approach allows us to
validate our model at multiple scales and there is very good agreement between simulation and experimental results at the fibril,
yarn, and sheet levels.
|
This model also takes into account the random misalignment of the fibrils due to the weaving process. This misalignment leads to
small variations in the yarn responses and creates a distribution of predicted yarn properties. By populating the macro-scale
fabric sheet with yarn from this distribution, the resulting overall model is a stochastic one. This leads to much more
realistic behavior of the simulated material where, even though the simulation may be geometrically symmetric, the overall
response is not. For example, in figure 1 failure occurs at some boundaries before others, replicating what we see in the
experimental tests.
This work is funded by the Army Research Laboratory through the Army High Performance Computing Research Center (cooperative
agreement W911NF-07-2-0027).
 |
| Figure 2: Multi-scale construction of fabric. |
|

