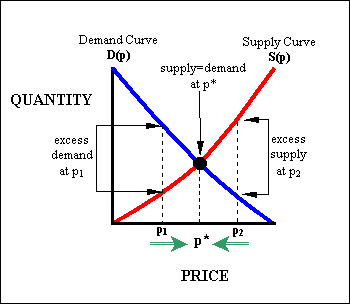
Figure 1: A supply-and-demand model of market prices
A number of authors have introduced some very esoteric and theoretical topics to popular culture: Chaos, complexity, fractals, non-linear systems, emergent properties and networks. These authors display for us surprising commonalities between evolution, ecologies, brains, human interactions, and the internet – power laws, far-from-equilibrium dynamics, and simplicities that emerge from systems of enormous, unmanageable complexity. The message: Everything and everyone are interconnected, and simple laws can describe how it all evolves through time.
David Batten follows in kind in his book, Discovering Artificial Economics: How Agents Learn and Economies Evolve[1]. He seeks to demonstrate how a few simple, unifying, ubiquitous laws of nature can describe the collective behavior of humans. He describes how the populations of United States cities, fluctuations in stock market prices, and the distribution of wealth all conform to power laws.[2] He demonstrates how many economic systems, from road traffic flows to financial markets, evolve abruptly and unpredictably, always in fluctuation, never resting in a steady state. He argues that economic agents are interconnected and interdependent, so that we cannot understand one person’s decisions in isolation from the behavior of everyone else.
Batten’s primary goal, however, is not just to highlight the ubiquitous laws that tie economic systems together. His goal is to convince his readers that to fully understand these ubiquitous, simple laws, we must first understand how these laws are determined by the beliefs and behaviors of many individual agents.
But standard economic theory will not suffice for the job, Batten argues. Standard economic theory, largely built on mathematical models of idealized, perfectly rational agents, has been unable to correctly predict the behavior of many real-life economic systems. Batten proposes a new field of study to fill in the gaps left by standard economic theory: “Artificial Economics.” Artificial Economics would employ computer simulations to model how the beliefs and behaviors of many interacting agents evolve into complex economic systems.
To understand the need for a new field of study like Artificial Economics, we should first clarify what Batten finds lacking in the field of Economics. Economics, he claims, is limited by its dependence on the concept of equilibrium. A system is said to reach an equilibrium state when some properties of the system will forever afterward remain constant, put simply. If you drop a marble into a bowl, the marble will eventually come to rest at the middle of the bottom of the bowl – the equilibrium state. Once resting there, the marble on its own will never move away from that point. If you give the marble a little push, it will eventually return to the equilibrium state at the bottom.
As Batten writes, “[Economics’] central dogma still revolves around stable equilibrium principles. Goods and services are assumed to flow back and forward between agents in quantifiable amounts until a state is reached where no further exchange can benefit any trading partner. Any student of economics is taught to believe that prices will converge to a level where supply equates to demand.”[3] Figure 1 below shows the kind of supply-and-demand model of prices found in every microeconomics textbook:

The “demand curve” D(p) represents the total desire of many potential buyers of some product. The buyers’ demand for the product decreases as the price of the product rises. The “supply curve” S(p) represents the amount of the product that would be created by some supplier. The supply of the product would increase as the price of the product increases, since higher prices allow producers to create more products to sell.
Suppose the price of the product were p1. The demand curve is higher than the supply curve at p1 (D(p1) > S(p1)), so the buyers will demand more products than are available. Suppliers of the product would want to increase the price to reap more profits, allowing them to increase the supply of the product to satisfy the buyers’ demand. As long as supply does not meet demand (D(p) > S(p)), suppliers would continue to raise the price p (see the arrow à).
But what if the price is increased to p2, greater than p*? Here, since S(p2) > D(p2), there is too much supply of the product and not enough demand to buy it all up. Suppliers will want to decrease the price to raise demand and cut costs by producing less of the product. As long as there is an excess of supply, suppliers will continue to decrease the price (see the arrow ß).
Whether the price starts at p1 < p* or at p2 > p*, the suppliers of the product will naturally change the price until the price is p*, the point at which supply exactly meets the demand for the product (S(p*) = D(p*)). This price p* is called the equilibrium price. According to this supply-and-demand model, the price will remain at p* in the long run, for as long as S(p) and D(p) still accurately represent the quantities of a product supplied and demanded for a price p, respectively.
Much of microeconomic theory reaches conclusions about long-run market behavior using models like this supply-and-demand model. Batten, however, takes a stand against these supply-and-demand models. He questions microeconomists’ implicit assumption that supply and demand curves (S(p) and D(p)) do not change as the market price shifts toward an equilibrium price: “It’s remarkable that the fallacy of a simple supply-demand equilibrium has persisted for so long. In the medium to long run, supply and demand functions cannot be specified in isolation of one another. They’re not independent functions of price. Each depends crucially on chance events in history – like the way in which fads start, rumors spread, and choices reinforce one another. Supply and demand affect each other, as well as being subject to common factors like the media.”[4] For Batten, supply and demand curves themselves fluctuate over time, so the equilibrium price p* at which S(p*) = D(p*) will fluctuate as well. Prices might shift in the real world quite differently than as predicted by the equilibrium model of microeconomics.
Batten points to the stock market as an example of where the equilibrium models of microeconomics predict price fluctuations inaccurately. Batten claims that “the vast majority of academics” accept a hypothesis called the “efficient market hypothesis” as the way prices in real markets change.[5] The efficient market hypothesis assumes that investors’ demand for a stock is determined by all available information about the performance of the company represented by the stock. The price is assumed to sit, on average, where the stock’s supply and demand will be equal – just like in the textbook supply-and-demand model above. The hypothesis is that in an “efficient” market, any new information about the company immediately will change investors’ demand for the stock, and the equilibrium price will adjust accordingly. Because good and bad news about any stock in the stock market will appear randomly, price fluctuations should follow a normal distribution, at least while the overall economy does not rise or fall.[6]
Contrary to the predictions of the efficient market hypothesis, prices of stocks in the New York Stock Exchange (and in many other financial markets) do not appear to fluctuate according to a normal distribution. Both Ralph Elliott[7] and Benoit Mandelbrot[8] noticed repeating patterns in short-term stock price fluctuations that disobey a normal distribution. If price fluctuations followed a normal distribution, then large changes in price from day to day would almost never occur; as Mandelbrot notes, the probability that large fluctuations will occur at any time is equal to “a few millionths of a millionth of a millionth of a millionth.” But the observed probability of such large fluctuations appears closer to 1/100, since large day-to-day fluctuations in one stock’s price occur almost every month.
Short-term price fluctuations instead are observed to follow a power law distribution,[9] not a normal distribution. Stock market price fluctuations would then have the “scale-free” property of all power law distributions, meaning that prices do not fluctuate around any average price. The efficient market hypothesis assumed that prices would fluctuate around an equilibrium price until new information changes investors’ demand. But in actuality, stock prices are always shifting, and there is rarely any price we can call the “equilibrium price” of a stock.
Batten believes the efficient market hypothesis’ flaw lies in its assumption that investors’ demand for a stock is changed only by outside information about the company. Batten found the same flaw in supply-and-demand models of market prices, which also held constant the demand curve, even while prices changed. He writes, “The basic problem with the efficient market hypothesis . . . is that [it concentrates] exclusively on the security itself and the information relating to it. The demand side of the market is trivialized. All idiosyncrasies of human nature are ignored.”[10] Batten believes that in reality, investors decide whether to buy a stock at a certain price for any number of assorted reasons. Some play the stock market for short-term gains; others dig in for the long haul.
Some investors are called “Fundamentalists,” who monitor the supply and demand of a stock to predict its future price. Consistent with the efficient market hypothesis, these investors believe that an equilibrium price exists where supply meets demand, and that demand is determined by outside information about a company’s performance. They expect the equilibrium price to change only upon hearing new information that will affect other investors’ demand. But without any new information to predict a company’s future performance, fundamentalists will see price shifts away from the equilibrium price as only temporary.
The fundamentalists’ strategy for investing in the stock market imposes a negative feedback on price fluctuations. If fundamentalists watch a stock’s price rise above its equilibrium price, they will predict that the price should eventually fall back to the equilibrium price. To capitalize on the temporary price increase, some fundamentalists will sell their shares – a move that on its own pushes the stock’s price down toward the equilibrium. If the price falls below the equilibrium price, fundamentalists will predict that the price will soon return to the equilibrium. Some will buy more shares of the stock, helping to push prices back up. Prophesying that a price will return to some equilibrium price, fundamentalists’ buy and sell stocks in ways that help the price return to equilibrium, helping to fulfill their own prophecies.
Another group of investors are called “technical traders,” who believe that the history of a stock’s price provides valuable information about how it will change in the future. They watch for patterns and trends in how a price fluctuates to predict where the price will end up. Their strategy runs counter to the efficient market hypothesis, since predictions can be based on changes in the price alone, independently of any information about the company itself.
The investment strategy of technical traders imposes a positive feedback on price fluctuations. If the price of a stock has fallen for several days, often technical traders will expect the price to keep falling. Some will sell their own shares before the price drops too low for comfort – a move that pushes the stock’s price even further down. Similarly, sometimes technical traders will see a rising stock price as a sign of more good to come. Some will buy shares of the stock to jump on the bandwagon, helping to boost the stock’s price even further! This effect was prominent during the 1990s, when Internet stock prices rose sharply (and fell) because more and more investors jumped onto (or off) the dot-com bandwagon. Thus, technical traders also can fulfill their own prophecies: Expecting a trend in a stock’s price to continue for good or for bad, technical traders buy and sell stocks in ways that help keep the trend going.
When predicting stock price movements from trends and patterns they find, technical traders are assuming that other investors also invest according to trends in stock price movements. They must assume that, to some extent, the efficient market hypothesis is not true, and that prices will not always return to an equilibrium. The technical traders, whose strategies create positive feedbacks that push prices away from equilibria, render the efficient market hypothesis false!
Since both fundamentalists and technical traders exist in large numbers in the real world of investment, price fluctuations in the stock market are driven by a complex mix of negative and positive feedback loops. Batten urges us to remember these complexities when forming models of financial markets. We certainly should remember that both fundamentalists and technical traders exist in the real world. Because of the positive feedbacks created by technical traders, initially small trends in price movements could quickly become the large price movements that Mandelbrot observed. Thus, including technical traders in our models will help fill the gaps in explaining the power law distribution of price fluctuations.
Batten argues convincingly that we must understand the behavior of individual investors in financial markets if we want to understand how those markets will evolve. Only by understanding the strategies of real-life investors in the stock market can we hope to predict how stock prices will fluctuate. The flaw of the efficient market hypothesis is its oversimplification of how investors evaluate a stock, according to Batten. Instead, he hopes that we will enrich our models of investors’ behavior and seek predictions about prices when they are fluctuating, not just standing still in equilibrium.
However, it is not clear that equilibrium models are fundamentally incapable of modeling price fluctuations. Batten cites the discovery of power law distributions in many different systems as unexpected and unfamiliar territory to economic modeling. Batten himself, however, proposes that the power-law distribution could be understood as a type of stable equilibrium. He shows us how the relationship between the population of US cities and their relative size ranks has been a power-law throughout the country’s history. He speculates, “The rank-size distribution seems to be an attractor in the phase space of all possible dynamics governing urban change. This suggests, but falls short of proving, that individual towns and cities self-organize in such a way that they preserve this rank-size pattern over time.”[11] But if the rank-size power law distribution is indeed a stable attracting equilibrium as he suggests, then the mathematical equilibrium models economists use should be able to model power law distributions in city sizes. Power laws, as well as many other complex or chaotic phenomena, will become familiar territory to economists once more of them set their sights on such phenomena.
Batten believes that positive feedbacks have been intentionally neglected by economics: “Most [economists] have refused to tackle the complexities of increasing returns economics, preferring to deny their importance. Given the lack of attention devoted to them, it’s surprising to find that positive feedback processes are so ubiquitous in societies.”[12] Nevertheless, a growing literature in economics now is trying to deal with positive feedbacks, path-dependence, technological lock-in, and network effects.
The equilibrium models that Batten knocks down are easy targets for criticism. The supply-and-demand model of market pricing and the efficient market hypothesis in financial markets are meant to overlook many features of real-life market behavior. But the rest of economics – all that is written after the basic supply-and-demand model in microeconomics textbooks, and all that is published in countless pages of economics journals – is mostly devoted to modeling the real-life economic world. Economists would certainly do well to listen to Batten’s message: Positive feedbacks, power laws, non-equilibrium fluctuations, and other complex phenomena are more common in economic systems than we expected. Nevertheless, we ought not lose faith in economic theory prematurely. It has carried us this far, and it will probably prove a trusty steed in the future too.
Standard economic theory has encountered a number of cases in which something is true for any individual but false for a group of individuals. Paul Samuelson lists a couple cases that economics has thus far encountered:[13]
Each case might seem paradoxical on the surface, since the consequences of any individual’s behavior are very different from the consequences of everyone behaving that way.
However, Batten writes that paradoxical statements like these “hardly scratch the surface compared to the full set of paradoxes that can arise. Furthermore, they’re a select group that can be resolved using the conventional static equilibrium view of the economy.”[14] Economics treats these cases as exceptions to the rule, but Batten thinks such cases are actually quite commonplace in economic systems.
Batten explains why observing individual agents often cannot explain how the whole system of interacting agents will behave. To illustrate why this is true, imagine three billiard balls bouncing across a pool table. Their paths would be predictable enough. Now imagine what would happen if we rolled 50 billiard balls across the pool table at once. Predicting the paths of individual balls would become intractable – or next to impossible. But we could predict average properties of the billiard balls, like their average velocity or average time between collisions. Properties of the entire system become predictable as properties of the individuals become intractable.
Batten believes that when few economic agents interact, the patterns of their collective behavior can be predictable with simple mathematical models. But whenever many different agents interact at once – which occurs in a very large class of economic systems – the interactions between agents become too complex to predict individually. Instead, generic properties of the system emerge from the underlying interactions between individuals.
Batten’s most controversial argument throughout the book is this: The mathematical models economists have used for centuries will not be able to predict the global properties of interacting agents in a large class of real-life economic systems. We must instead use computer simulations, he proposes, to model all the complexities of individual, interacting agents to see what system-wide properties emerge.
One convincing example of where Batten thinks computer simulations should supplant mathematical models is in the analysis of traffic on roads and highways. A Nobel laureate in economics, William Vickrey[15], analyzed traffic flows using a mathematical function relating traffic on a road to the time it takes to drive down the road, called a “link performance function.” For instance, if f is the flow of traffic on a road (measured in vehicles/second), then the time it takes any one of the cars to drive down the road would be T(f) = T0 + a·fk, where T0 is the travel time without any traffic flow, and a and k are constants.
Now, suppose that during every minute, 20 drivers wish to drive from some location A to location B, and they can take one of two possible roads to get there (see Figure 2).
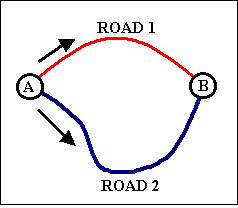
There would be a different link performance function for each road: T1(f) = T01 + a1·fk1 describes the time it takes to drive down road 1 given the traffic flow f on that road, and T2(f) = T02 + a2·fk2 describes the time it takes to travel down road 2.
Now, assume that every driver knows these two link performance functions T1(f) and T2(f) and his goal is to minimize his travel time from A to B. Each driver would switch from road to road, day after day, trying to find the road that will minimize T(f) given the traffic flow f on that road. Each driver’s decision affects the traffic flow on both roads by increasing congestion on one road but relieving congestion on the other road. Eventually though, every driver will find a route he likes. Here, switching roads would only increase his travel time if all other drivers stick with their current routes. This state of traffic on the two roads is called the “user equilibrium” – an equilibrium state in which no driver would prefer to switch routes, given the routes chosen by all other drivers.
However, we might wonder: Is the user equilibrium necessarily the state of traffic flow that minimizes the total travel time of all drivers? The answer to this question is No. The pattern of traffic flow that minimizes the total travel time of all drivers is known as the “system optimum.” Braess’ Paradox denotes a broad set of cases in which the system optimum does not coincide with the user equilibrium.
To demonstrate Braess’ Paradox, Figure 3 shows two possible link performance functions T1(f) and T2(f) for the roads 1 and 2 depicted in Figure 2.
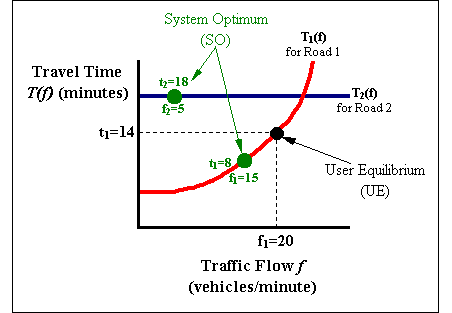
Knowing the link performance functions T1(f) and T2(f) shown in Figure 3, each driver will seek the quickest route from location A to B. According to Vickrey’s analysis, eventually all the drivers’ choices of routes will settle on the user equilibrium (UE), where all 20 drivers choose to take Road 1 because Road 2 would only increase his travel time. When 20 vehicles per minute are using Road 1, it takes each driver 14 minutes to drive from A to B. Thus, the total time to travel from A to B is 280 minutes for each group of cars.
The system optimum (SO) for this road configuration, however, differs from the UE. If several drivers would cooperate and switch to Road 2, the rest of the drivers would benefit from an emptier Road 1. If at every minute, five drivers all together were to switch to Road 2, their travel time would increase to 18 minutes. But now, it would only take eight minutes for the other 15 drivers to drive down Road 1, and the total travel time of the group would only be 210 minutes.
The fact that the user equilibrium does not always coincide with the system optimum is Braess’ Paradox. As Batten points out, Braess’ Paradox is only paradoxical to those who assume that routes picked by self-interested drivers will always minimize the total driving time for everyone, even if every driver does not consider how his choice of routes affects the other drivers.
For Batten, the confusion comes from assuming that self-interested drivers will choose routes without considering how other drivers will choose routes. He writes, “[A] fundamental question remains to be answered. Can we realistically expect a user equilibrium to be stable, even reachable, in practice? Or is Braess’ Paradox symptomatic of the uncertainties associated with network connectivity, link congestability, and drivers’ travel choice behavior?” Batten wants our models to dig deeper into the strategies of real-life drivers: “How do drivers respond in situations where their own behavior is also dependent on the behavior of others? Do variations in travel time cause them to alter their decision rules?”[16]
One survey of 4,000 drivers in Seattle conducted by the University of Washington, for example, indicates several strategies that different groups of drivers use: some drivers never change routes, some drivers adjust to the traffic they encounter, and others try different routes out every day. We should include diversity in drivers’ behaviors in our models, Batten argues, rather than use simplified, unrealistic models of human behavior that happen to be convenient to analyze mathematically.
Batten believes that we need to employ computer simulations to be able to understand how the efficient flow of traffic is determined by the behaviors of individual drivers and the ways that drivers affect each other. Several computer simulations of traffic flows indicate a very surprising result.[17] When the density of traffic flow is very low (say, less than 10% of the total capacity of the road), every driver can drive relatively fast. But when the density of traffic flow increases a little bit (say, to 30% of total capacity), traffic discontinuously changes from freely flowing traffic to stop-and-go traffic. Drivers suddenly face large fluctuations in their speeds, and their average speed drops. This sudden change in the flows of traffic runs counter to Vickrey’s link performance functions, which assume that drivers’ speeds change continuously as traffic flow increases, and that large fluctuations in speeds simply do not occur.
Batten highlights another computer simulation of traffic flows in Albuquerque, New Mexico called “TRANSIMS”, created by researchers at Los Alamos.[18] TRANSIMS models drivers as complicated agents constantly adapting to driving conditions, like local congestion and accidents. TRANSIMS allows these researchers to study how properties of the entire traffic system of Albuquerque are determined by the behaviors of individual agents, the layout of roads, the environment, and many other contributing factors.
Batten hails this kind of research for accurately modeling the complexities of individual agents, and thus allowing us to reach accurate conclusions about the system as a whole: “The true representation of a higher-level simplicity emerges only as an explicit consequence of an accurate representation of its lower-level compexities.”[19] Batten argues, again and again, that in order to model the behavior of complex economic systems accurately, we will need to model the behavior of individual economic agents realistically.
Real-life agents in real-life economies make decisions based on imperfect knowledge of their surroundings and of other agents. When many agents are interacting in real-life, no agent can predict how all the other agents will behave. Whether stuck in traffic or buying shares on the stock market, different agents use different strategies for finding the optimal action to take as they observe the behaviors of others. Our job of understanding the collective system of interacting agents is quite a difficult one. According to Batten, analytic economic models of simple, rational agents will not suffice for dealing with the complexity and uncertainties in real-life economic systems.
Batten’s envisions a new field called “Artificial Economics.” Artificial economics would use agent-based computer simulations to “build” economic systems from the ground-up. Economic agents would be endowed with a diversity of lifelike economic behaviors. Many agents would interact simultaneously in an artificial economic environment. The computer simulations would allow us to discover exactly how the behavior of a whole system depends on the behaviors of individual agents. Batten writes, “Agent-based simulation allows one to explore an economic system’s behavior under a wide range of parameter settings and conditions. The heuristic value of this kind of experimentation cannot be overestimated. One gains much richer insights into the potential dynamics of an economy by observing the behavior of its agents under many different conditions.”[20]
Agent-based computer simulations are good tools for showing us how systems of agents behave, and they will undoubtedly provide many novel discoveries for economists to chew on. We can watch a simulation run and reach interesting qualitative conclusions. But for discoveries made through Artificial Economics to ever seriously challenge standard economic theory, it will first have to substantiate its discoveries. Artificial Economics will have to reach precise, quantitative conclusions that can be compared with empirical data in the real world. Once Artificial Economics can present precise conclusions that enable us to make predictions about economies that we could not make before, then people will listen to what Artificial Economics has to say.
TRANSIMS, for example, modeled the transportation system of a simulated Albuquerque, New Mexico. It demonstrates how transportation in the city changes as a result of changes in traffic patterns, the environment, and several other factors. However, the creators of TRANSIMS should try to reach quantitative conclusions substantiated by data collected from the real city of Albuquerque. Only then – when the conclusions reached through TRANSIMS are exacting and well-substantiated – will these researchers be able convince anyone to alter the traffic system in the city of Albuquerque.
Batten’s vision is ambitious but certainly realistic. To cope with the complexity of economic systems, we will need to use agent-based computer simulations. Using mathematical formulas to predict how many interacting agents behave becomes an intractable ordeal very quickly. Computer models, in contrast, can track the behaviors of many interacting agents simultaneously and with great precision. They can show us how an economic system would behave if people behaved one way or another. Discovering Artificial Economics does a good job convincing its readers that in the future, many important contributions will come from agent-based computer simulations, which have only just begun to be introduced to the field of economics.
This book review was written March 18, 2003, for the Symbolic Systems 205 class at Stanford University: “Systems: Science, Theory, Metaphor.” For details about the class, please see: http://www.stanford.edu/class/symbsys205/.
[1] Batten, David F. (2000) Discovering Artificial Economics: How Agents Learn and Economies Evolve. Westview Press.
[2] A system conforms to a “power law” when the logarithm of two properties of the system are linearly related. That is, the power law P1 = c×P2-d holds for two properties P1 and P2 (and constants c and d) when log(P1) is linearly proportional to log(P2). In the case of the populations of US cities (see pp.163-8), P = c×R-d is the power law where P=population of a city and R=rank of that city’s population (i.e. R=1 for New York, R=2 for Los Angeles, R=3 for Chicago, and so on).
[3] Batten, p.5
[4] ibid., p.109
[5] ibid., p.210
[6] For more information about random fluctuations of stock prices, see http://www.sciencenews.org/sn_arc99/2_20_99/mathland.htm
[7] Frost, A.J., and R.P.Prechter. (1990) Elliott Wave Principle: Key to Stock Market Profits. Gainesville, GA: New Classics Library.
[8] Mandelbrot, B. (1999) “A Multifractal Walk Down Wall Street.” Scientific American, February, pp. 50-53. Found at: http://www.elliottwave.com/education/SciAmerican/Mandelbrot_Article2.htm (Mandelbrot’s 1999 article stirred up some controversy by neglecting to give credit to Elliott, who saw the same fractal patterns in the Stock Market in 1938. See http://www.elliottwave.com/education/SciAmerican/credit_where_it_is_due2.htm)
[9] According to a power law for price fluctuations, the probability of a fluctuation f occurring from one day to the next would be: P(f) = c•f--d, for some constants c and d
[10] Batten, p.212
[11] ibid., p.167 (emphasis in italics in this quote comes from the original)
[12] ibid., p.36
[13] Samuelson, P. (1976) Economics. New York: McGraw-Hill, p.14.
[14] Batten, p.83-4
[15] Vickrey, D.S. (1969) “Congestion Theory and Transport Investment.” American Economic Review, vol. 59, pp. 251-260.
[16] Batten, p.186-7
[17] ibid., p.191-2
[18] ibid., p.194. For details about TRANSIMS, see: http://transims.tsasa.lanl.gov/
[19] ibid., p.206
[20] ibid., p.259