Simple Linear Regression

STATS 191

2024-04-01

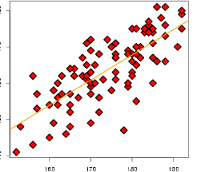
Father & son data

Pearson’s height data

Father & son data

• An example of simple linear regression model.

• Breakdown of terms:

  1. regression model: a model for the mean of a response given features

  2. linear: model of the mean is linear in parameters of interest

  3. simple: only a single feature

Slicewise model

• A simple linear regression model fits a line through the above scatter plot by modelling slices.

Conditional means

• The average height of sons whose height fell within our slice [69.5,79.5] is about 69.8 inches.

• This height varies by slice…

• At 65 inches it’s about 67.2 inches:

Multiple samples model (longevity example)

• We’ve seen this slicewise model before: error in each slice the same.

Regression as slicewise model

• In longevity model: no relation between the means in each slice! We needed to use a parameter for each Diet…

• Regression model says that the mean in slice father is

\[ \beta_0+\beta_1 \cdot {\tt father}. \]

• This ties together all (father, son) points in the scatterplot.

• Chooses \((\beta_0, \beta_1)\) by jointly modeling the mean in each slice…

Height data as slices

What is a “regression” model?

• Model of the relationships between some covariates / predictors / features and an outcome.

• A regression model is a model of the average outcome given the covariates.

Mathematical formulation

For height data: a mathematical model:

\[ {\tt son} = f({\tt father}) + \varepsilon \]

• \(f\) describes how mean of son varies with father

• \(\varepsilon\) is the random variation within the slice.

Linear regression models

• A linear regression model says that the function \(f\) is a sum (linear combination) of functions of father.

• Simple linear regression model:

\[\begin{equation} f({\tt father}) = \beta_0 + \beta_1 \cdot {\tt father} \end{equation}\]

• Parameters of \(f\) are \((\beta_0, \beta_1)\)

• Could also be a sum (linear combination) of fixed functions of father:

\[\begin{equation} f({\tt father}) = \beta_0 + \beta_1 \cdot {\tt father} + \beta_2 \cdot {\tt father}^2 \end{equation}\]

Statistical model

• Symbol \(Y\) usually used for outcomes, \(X\) for covariates…

• Model:

\[\begin{equation} Y_i = \underbrace{\beta_0 + \beta_1 X_i}_{\text{regression equation}} + \underbrace{\varepsilon_i}_{\text{error}} \end{equation}\]

where \(\varepsilon_i \sim N(0, \sigma^2)\) are independent.

• This specifies a distribution for the \(Y\)’s given the \(X\)’s, i.e. it is a statistical model.

Regression equation

• The regression equation is our slicewise model.

• Formally, this is a model of the conditional mean function

\[\begin{equation} x \mapsto E[Y|X=x] \end{equation}\]

• Book uses the notation \(\mu\{Y|X\}\).

Fitting the model

• We will be using least squares regression. This measures the goodness of fit of a line by the sum of squared errors, \(SSE\).

• Least squares regression chooses the line that minimizes

\[\begin{equation} SSE(\beta_0, \beta_1) = \sum_{i=1}^n (Y_i - \beta_0 - \beta_1 \cdot X_i)^2. \end{equation}\]

• In principle, we might measure goodness of fit differently:

  \[ SAD(\beta_0, \beta_1) = \sum_{i=1}^n |Y_i - \beta_0 - \beta_1 \cdot X_i|.\]

• For some other loss function \(L\) we might try to minimize

  \[ L(\beta_0,\beta_1) = \sum_{i=1}^n L(Y_i-\beta_0-\beta_1\cdot X_i) \]

Why least squares?

• With least squares, the minimizers have explicit formulae – not so important with today’s computer power.

• Resulting formulae are linear in the outcome \(Y\). This is important for inferential reasons. For only predictive power, this is also not so important.

• If assumptions are correct, then this is maximum likelihood estimation.

• Statistical theory tells us the maximum likelihood estimators (MLEs) are generally good estimators.

Choice of loss function

• Suppose we try to minimize squared error over \(\mu\):

\[ \sum_{i=1}^n (Y_i - \mu)^2. \]

• We know (by calculus) that the minimizer is the sample mean.

• If we minimize absolute error over \(\mu\)

\[ \sum_{i=1}^n |Y_i - \mu|.\]

• We know (similarly by calculus) that the minimizer(s) is (are) the sample median(s).

Visualizing the loss function

Let’s take some a random scatter plot and view the loss function.

Let’s plot the loss as a function of the parameters. Note that the true intercept is 1.5 while the true slope is 0.1.

Let’s contrast this with the sum of absolute errors.

Geometry of least squares

• Some things to note:

  1. Minimizing sum of squares is the same as finding the point in the X,1 plane closest to \(Y\).

  2. The total dimension of the space is 1078.

  3. The dimension of the plane is 2-dimensional.

  4. The axis marked “\(\perp\)” should be thought of as \((n-2)\) dimensional, or, 1076 in this case.

Least squares

The (squared) lengths of the above vectors are important quantities in what follows.

Important lengths

There are three to note:

\[\begin{equation} \begin{aligned} SSE &= \sum_{i=1}^n(Y_i - \widehat{Y}_i)^2 = \sum_{i=1}^n (Y_i - \widehat{\beta}_0 - \widehat{\beta}_1 X_i)^2 \\ SSR &= \sum_{i=1}^n(\overline{Y} - \widehat{Y}_i)^2 = \sum_{i=1}^n (\overline{Y} - \widehat{\beta}_0 - \widehat{\beta}_1 X_i)^2 \\ SST &= \sum_{i=1}^n(Y_i - \overline{Y})^2 = SSE + SSR \\ \end{aligned} \end{equation}\]

An important summary of the fit is the ratio

\[\begin{equation} \begin{aligned} R^2 &= \frac{SSR}{SST} \\ &= 1 - \frac{SSE}{SST} \\ &= \widehat{Cor}(\pmb{X},\pmb{Y})^2. \end{aligned} \end{equation}\]

• Measures how much variability in \(Y\) is explained by \(X\).

Case study A: data suggesting the Big Bang

Let’s fit the linear regression model.

Let’s look at the summary:

Hubble’s model

• Hubble’s theory of the Big Bang suggests that the correct slicewise (i.e. regression) model is

\[ \mu\{{\tt Distance} | {\tt Velocity}\} = \beta_1 \cdot {\tt Velocity} \]

• To fit without an intercept

Least squares estimators

There are explicit formulae for the least squares estimators, i.e. the minimizers of the error sum of squares.

For the slope, \(\hat{\beta}_1\), it can be shown that

\[ \widehat{\beta}_1 = \frac{\sum_{i=1}^n(X_i - \overline{X})(Y_i - \overline{Y} )}{\sum_{i=1}^n (X_i-\overline{X})^2} = \frac{\widehat{Cov}(X,Y)}{\widehat{Var}( X)}.\]

Knowing the slope estimate, the intercept estimate can be found easily:

\[ \widehat{\beta}_0 = \overline{Y} - \widehat{\beta}_1 \cdot \overline{ X}.\]

Example: big_bang

Estimate of \(\sigma^2\)

The estimate most commonly used is

\[ \begin{aligned} \hat{\sigma}^2 &= \frac{1}{n-2} \sum_{i=1}^n (Y_i - \hat{\beta}_0 - \hat{\beta}_1 X_i)^2 \\ & = \frac{SSE}{n-2} \\ &= MSE \end{aligned} \]

• We’ll use the common practice of replacing the quantity \(SSE(\hat{\beta}_0,\hat{\beta}_1)\), i.e. the minimum of this function, with just \(SSE\).

• The term MSE above refers to mean squared error: a sum of squares divided by its degrees of freedom. The degrees of freedom of SSE, the error sum of squares is therefore \(n-2\).

Mathematical aside

• We divide by \(n-2\) because some calculations tell us:

\[ \frac{\hat{\sigma}^2}{\sigma^2} \sim \frac{\chi^2_{n-2}}{n-2} \]

• Above, the right hand side denotes a chi-squared distribution with \(n-2\) degrees of freedom.

• Dividing by \(n-2\) gives an unbiased estimate of \(\sigma^2\) (assuming our modeling assumptions are correct).

Example: big_bang

Inference for the simple linear regression model

Remember: \(X\) can be fixed or random in our model…

Case study B: predicting pH based on time after slaughter

• In this study, researches fixed \(X\) (Time) before measuring \(Y\) (pH)

• Ultimate goal: how long after slaughter is pH around 6?

Inference for \(\beta_0\) or \(\beta_1\)

• Recall our model

\[Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i\]

• The errors \(\varepsilon_i\) are independent \(N(0, \sigma^2)\).

• In our heights example, we might want to now if there really is a linear association between \({\tt son}=Y\) and \({\tt father}=X\). This can be answered with a hypothesis test of the null hypothesis \(H_0:\beta_1=0\). This assumes the model above is correct, AND \(\beta_1=0\).

• Alternatively, we might want to have a range of values that we can be fairly certain \(\beta_1\) lies within. This is a confidence interval for \(\beta_1\).

A mathematical aside

• Let \(L\) be the subspace of \(\mathbb{R}^n\) spanned \(\pmb{1}=(1, \dots, 1)\) and \({X}=(X_1, \dots, X_n)\).

• We can decompose \(Y\) as

\[{Y} = P_L{Y} + ({Y} - P_L{Y}) = \widehat{{Y}} + (Y - \widehat{{Y}}) = \widehat{{Y}} + e\]

• In our model, \(\mu=\beta_0 \pmb{1} + \beta_1 {X} \in L\) so that

  \[ \widehat{{Y}} = \mu + P_L{\varepsilon}, \qquad {e} = P_{L^{\perp}}{{Y}} = P_{L^{\perp}}{\varepsilon}\]

• Our assumption that \(\varepsilon_i\)’s are independent \(N(0,\sigma^2)\) tells us that: \({e}\) and \(\widehat{{Y}}\) are independent; \(\widehat{\sigma}^2 = \|{e}\|^2 / (n-2) \sim \sigma^2 \cdot \chi^2_{n-2} / (n-2)\).

Setup for inference

• All of this implies

\[ \widehat{\beta}_1 \sim N\left(\beta_1, \frac{\sigma^2}{\sum_{i=1}^n(X_i-\overline{X})^2}\right).\]

• Therefore,

\[\frac{\widehat{\beta}_1 - \beta_1}{\sigma \cdot \sqrt{\frac{1}{\sum_{i=1}^n(X_i-\overline{X})^2}}} \sim N(0,1).\]

• The other quantity we need is the standard error or SE of \(\hat{\beta}_1\):

\[ SE(\widehat{\beta}_1) = \widehat{\sigma} \cdot \sqrt{\frac{1}{\sum_{i=1}^n(X_i-\overline{X})^2}} \qquad \text{independent of $\widehat{\beta}_1$}\]

Testing \(H_0:\beta_1=\beta_1^0\)

• Suppose we want to test that \(\beta_1\) is some pre-specified value, \(\beta_1^0\) (this is often 0: i.e. is there a linear association)

• Under \(H_0:\beta_1=\beta_1^0\)

  \[\frac{\widehat{\beta}_1 - \beta^0_1}{\widehat{\sigma} \sqrt{\frac{1}{\sum_{i=1}^n(X_i-\overline{X})^2}}} = \frac{\widehat{\beta}_1 - \beta^0_1}{ \frac{\widehat{\sigma}}{\sigma}\cdot \sigma \sqrt{\frac{1}{ \sum_{i=1}^n(X_i-\overline{X})^2}}} \sim t_{n-2}.\]

• Reject \(H_0:\beta_1=\beta_1^0\) if \(|T| > t_{n-2, 1-\alpha/2}\).

Example: big_bang

Let’s perform this test for the Big Bang data.

• We see that R performs our \(t\)-test in the second row of the Coefficients table.

• It is clear that Distance is correlated with Velocity.

• There seems to be some flaw in Hubble’s theory: we reject \(H_0:\beta_0=0\) at level 5%: \(p\)-value is 0.0028!

Why reject for large |T|?

• Logic is the same as other \(t\) tests: observing a large \(|T|\) is unlikely if \(\beta_1 = \beta_1^0\) (i.e. if \(H_0\) were true). \(\implies\) it is reasonable to conclude that \(H_0\) is false.

• Common to report \(p\)-value:

\[\mathbb{P}(|T_{n-2}| > |T|_{obs}) = 2 \cdot \mathbb{P} (T_{n-2} > |T_{obs}|)\]

Confidence interval for regression parameters

• Applying the above to the parameter \(\beta_1\) yields a confidence interval of the form

\[\hat{\beta}_1 \pm SE(\hat{\beta}_1) \cdot t_{n-2, 1-\alpha/2}.\]

• Earlier, we computed \(SE(\hat{\beta}_1)\) using this formula

  \[ SE(a_0 \cdot \hat{\beta}_0 + a_1 \cdot \hat{\beta}_1) = \hat{\sigma} \sqrt{\frac{a_0^2}{n} + \frac{(a_0\cdot \overline{X} - a_1)^2}{\sum_{i=1}^n \left(X_i-\overline{X}\right)^2}}\] with \((a_0,a_1) = (0, 1)\).

We also need to find the quantity \(t_{n-2,1-\alpha/2}\). This is defined by

\[ \mathbb{P}(T_{n-2} \geq t_{n-2,1-\alpha/2}) = \alpha/2. \]

In R, this is computed by the function qt.

We will not need to use these explicit formulae all the time, as R has some built in functions to compute confidence intervals.

Predicting the mean

Once we have estimated a slope \((\hat{\beta}_1)\) and an intercept \((\hat{\beta}_0)\), we can predict the height of the son born to a father of any particular height by the plugging-in the height of the new father, \(F_{new}\) into our regression equation:

\[ E[{S}_{new}|F_{new}] = \mu\{S_{new}|F_{new}\} = {\beta}_0 +{\beta}_1 F_{new}. \]

• Confidence interval for the average height of sons born to a father of height \(F_{new}=70\) (or maybe \(65\)) inches:

\[ \hat{\beta}_0 + 70 \cdot \hat{\beta}_1 \pm SE(\hat{\beta}_0 + 70 \cdot \hat{\beta}_1) \cdot t_{n-2, 1-\alpha/2}. \]

Computing \(SE(\hat{\beta}_0 + 70 \cdot \hat{\beta}_1)\)

• We use the previous formula

  \[ SE(a_0\cdot \hat{\beta}_0 + a_1\cdot\hat{\beta}_1) = \hat{\sigma} \sqrt{\frac{a_0^2}{n} + \frac{(a_0\cdot \overline{X} - a_1)^2}{\sum_{i=1}^n \left(X_i-\overline{X}\right)^2}}\] with \((a_0, a_1) = (1, 70)\).

• Plugging in

\[ SE(\hat{\beta}_0 + 70 \cdot \hat{\beta}_1) = \hat{\sigma} \sqrt{\frac{1}{n} + \frac{(\overline{X} - 70)^2}{\sum_{i=1}^n \left(X_i-\overline{X}\right)^2}} \]

• As \(n\) grows (taking a larger sample), \(SE(\hat{\beta}_0 + 70 \hat{\beta}_1)\) should shrink to 0. Why?

Forecasting / prediction intervals

• Can we find an interval that covers the height of a particular son knowing only that her father’s height as 70 inches?

• Must cover the variability of the new random variation \(\implies\) it must be at least as wide as \(\sigma\).

With so much data in our heights example, this 90% interval will have width roughly \(2 \cdot 1.96 \cdot \hat{\sigma}\)

Formula

• Actual width will depend on how accurately we have estimated \((\beta_0, \beta_1)\) as well as \(\hat{\sigma}\).

\[ SE(\widehat{\beta}_0 + \widehat{\beta}_1 \cdot 70 + \varepsilon_{\text{new}}) = \widehat{\sigma} \sqrt{1 + \frac{1}{n} + \frac{(\overline{X} - 70)^2}{\sum_{i=1}^n \left(X_i-\overline{X}\right)^2}}. \]

The final interval is

\[ \hat{\beta}_0 + \hat{\beta}_1 \cdot 70 \pm t_{n-2, 1-\alpha/2} \cdot SE(\hat{\beta}_0 + \hat{\beta}_1 \cdot 70 + \varepsilon_{\text{new}}). \]

• Computed in R as follows