• Introduction
• Background
• Results and Analysis
• Implementation Issues
• Conclusion

---

Introduction

This work is to compare the performance of two different pyramid coding for still images: a critically sampled subband pyramid and an over-complete pyramid. Once the coefficients of subbands or the error signals in different layers are obtained, the way they are quantized and encoded affects the efficiency of compression significantly. Since we focus on the rate-distortion performance and bit allocation in this work, we implement simple scalar quantizers and memoryless encoding, with optimized bit allocation for the coefficients.

In the following sections, we will briefly discuss the two subband pyramid coding schemes, bit allocation and quantization. How these are implemented in this work is also described in detail. The simulation results are presented and analyzed with a few testing images.

---

Background

1. Critically Sampled Pyramid

   In critically sampled pyramid coding, the image spectrum is decomposed into subbands by analysis filters. The filtered signal is then subsampled by a factor of 2 such that the cascaded decomposition operation results in the same number of samples as that of the original image. Due to the delaying property of the typical image spectrum from low frequency to high frequency, the decomposition produces subbands with flatter spectrum. Encoding these subbands with greatly reduced statistical correlation improves the coding efficiency according to the rate distortion theory [4].
   
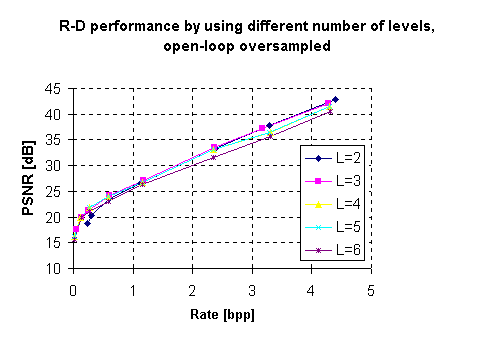
   In this work we choose the octave-band decomposition over the uniform decomposition. Since the decay of the typical spectrum is more rapid at lower frequencies, the former yields subbands with even flatter spectrum by dividing lower bands further into smaller bandwidth. Discrete Wavelet Transform (DWT) is a common method to implement octave subband decomposition, which has been employed in this work for critically sampled pyramid coding. Fig. 1 shows the original image and the signal decomposed  by analysis filters cascaded in three levels, which results in ten subbands. The lowest band is shown at the top left corner in the bottom image in Fig. 1 , where the energy is mostly concentrated.
   
   

   
   Fig. 1. Mandrill (256x256): original image (top) and 10 subbands by DWT (bottom).
   
   
   
2. Overcomplete Pyramid

   Besides critically sampled pyramid, overcomplete pyramid decomposition technique is frequently used. This was introduced as a simple, yet powerful image representation scheme by Burt and Adelson [7]. From the original image, a low-resolution version is derived, then the original is predicted based on the coarse version, and the difference is calculated between the original and the prediction. At the decoder, the prediction is simply added back to the difference. Of course, the process can be iterated on the coarser version. Fig. 2 shows 3-layered over-complete pyramid. The upper one is the coarser version and the other two are prediction error signals.
   
   

   
   
   
   
   Fig. 2. Mandrill (256x256): 3-layered encoded signals in overcomplete pyramid: low-resolution image (top) and error signals (bottom).
   
   
   A shortcoming of this scheme is the oversampling, in other words, the number of encoded pixels is greater than that in the original image. Assume we start with an image. After one step, we have an coarse version, but also an difference image. If the scheme is iterated, we have the following number of samples:

   

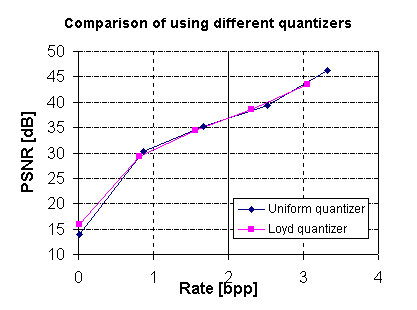
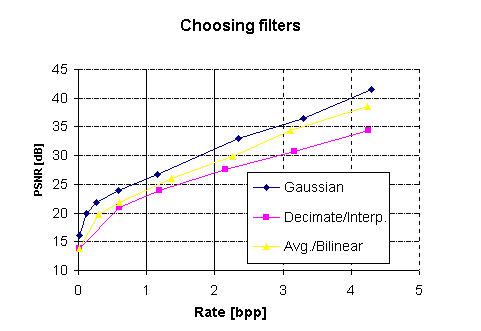
   The benefit of the oversampled pyramid comes from the fact that arbitrary filters (including nonlinear ones) can be used, and that visually pleasing coarse versions are easy to obtain by choosing unconstrained filters for decimation and interpolation. We tried three different filters: Gaussian filter as in the original Burt and Adelson scheme [7], simple averaging and bilinear interpolation filter suggested in [3], and Chebyshev type I lowpass filter generated by Matlab built-in functions "decimate" and "interp". Gaussian filter is used for later experiments to be shown since it gives the best rate-distortion performance among the three, which is illustrated in Fig. 3.

   
   
   Fig. 3. RD curve for different decimation and interpolation filters.
   
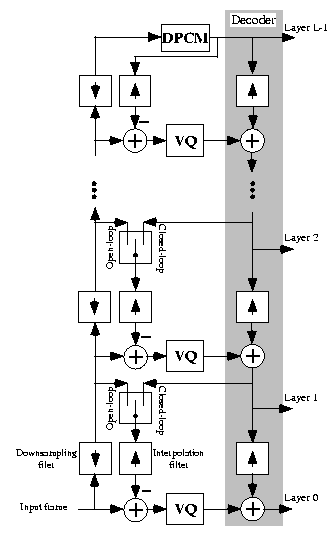
   In this work we implement both open-loop and closed-loop pyramid structure introduced in [3]. The block diagram of N-layer pyramid codec is shown in Fig. 4 which is taken from [3].
   
   
   
   
   
   
   Fig. 4. N-layer pyramid codec: Open-Loop and Closed-Loop.
   
   
   

3. Quantization and Bit Allocation

   In both critically sampled pyramid and oversampled pyramid, quantization is performed on the coefficients of subbands or the error signals of the over-sampled layers to compress the signal. In order to encode the image with maximum efficiency, different bit rates should be assigned to each subband or layer, depending on its statistical property. Here we will first review the bit allocation scheme in an analytical way and then discuss a "greedy" algorithm used in practice.
   
   3.1 Analytical solutions
   

   We denote the allocated bit rate per pixel in layer l or subband l by r_l, then the bit rate for the image is

   ,                              (1)

   where is the ratio of number of samples in layer l or coefficients in subband l over that of the full resolution layer. The distortion (per pixel) in layer l or subband l is denoted by D_l, and the distortion of full resolution layer is

   .                             (2)

   To have the minimum distortion given the bit rate constrain r, one can obtain

   , and

                            (3)

   According to the detailed analysis in [3], the optimal bit allocation for subband l in the critically sampled case, or layer l in the open-loop oversampled case is

   ,         (4)

   where ,  is the power transfer factor, is the spectral flatness and is the variance of the interpolation error signal.

   For the closed-loop oversampled case,

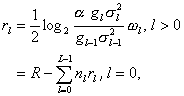   where
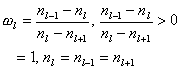   .       (5)  

   
   

   From the above, (4) and (5) are the analytical forms we follow in our simulations for bit allocation.

   
   3.2 The "greedy" algorithm
   
   The problem with the analytical bit allocation scheme is that the rates might be noninteger or negative [2]. Another algorithm tackles the bit allocation problem by directly following (3), independent of any analytical form of the image statistics. That is, at each time, allocating one more bit to the subband or layer which results in the maximum reduction in distortion. This iteration will continue until the all the bits under the constraint have been consumed. This scheme is usually called the "greedy" algorithm. It is not optimal, since by allocating one bit to each subband or layer at each time, the relationship in (3) is not guaranteed when the iteration stops. This algorithm is applicable in practice though. We will show the performance by these two algorithms in the next section.
   
   

---

Results and Analysis

1. Rate-distortion performance
   
   Fig. 5 shows the rate-distortion performance of critically sampled and oversampled pyramid coding. The results are obtained form encoding the ensemble of the five testing images mentioned above. We use three layers for subband coding and decompose the image into ten octave subbands. We use four layers in oversampled pyramid coding. Two bit allocation algorithms are applied on critically sampled and open-loop oversampled pyramids. Since in closed-loop pyramids, distortion in one layer depends on all the previous quantizers, the bit allocation by greedy algorithm will be more complicated. We only use analytical solution for closed-loop pyramids.
   
   
   
   
   Fig. 5. Rate-distortion performance of critically sampled and oversampled pyramid coding
   
   
   In general, the performance of critically sampled coder outperforms oversampled one in terms of rate-distortion. The critically sampled pyramid saves approximately 0.4 bit to achieve the same 25 dB PSNR, and this difference is even bigger for high bit rate. The PSNR difference is approximately 4 dB at 0.5 bpp and 8 dB at 2 bpp. This is because in the oversampled scheme, there are more samples than in the original image to encode, while the improved PSNR does not complete reward the encountered overhead of the increased number of samples and bit rate. However, this indicates that oversampled pyramid is more suitable for low bit-rate coding.
   
   The closed-loop shows slight better performance over the open-loop method due to the noise feedback used and the gap gets bigger for higher bit rates.
   
   In both schemes of critically sampled and oversampled pyramids, although the greedy algorithm of bit allocation is not optimum, its performance is nearly as good as that by using the analytical solution. In later simulations to be shown, we use the greedy bit allocation algorithm.
   
   
2. Scalability
   
   One important feature we desire from pyramid coding is the scalability. In this subsection we will compare the scalability provided by critically sampled and oversampled pyramids.
   
   First we look at the subjective quality of images reconstructed from full resolution layers and lower resolution layers. As what we've seen in the previous subsection, the critically sampled scheme gives better performance over the oversampled scheme in terms of R-D performance. Because of this, we compare the quality of the images reconstructed with the same PSNR at the full resolution layer, being aware that the oversampled scheme uses more bits.
   
   We performed the simulation on the 256x256 Einstein image, with 3 layers (10 subbands) for critically sampled, and 4 layers for open-loop oversampled pyramids. As a result, in both cases, we are able to reconstruct images from levels 0 (full resolution), 1, 2, and 3 (coarsest resolution).
   
   
   Table 1. Images reconstructed from different layers and with critically sampled and oversampled pyramids
   
   

   Full resolution layer PSNR (dB)	Pyramid	Pyramid
   28	Critically sampled	Oversampled
   30	Critically sampled	Oversampled
   33	Critically sampled	Oversampled

   
   
   
   From the six sets of images shown above we can observe that for the same lowest PSNR of 28 dB, the oversampled pyramid results in better perceptual image quality than that by critically sampled pyramid, although the two schemes give the same full resolution PSNR. The ripples in the images reconstructed from critically sampled pyramids do not show in those from their oversampled counterparts. As the PSNR of full resolution images increases, the advantage of oversampled pyramid over the critically sampled one becomes less obvious, since images with higher PSNRs tend to give good quality with little perceptual difference.
   
   In Fig. 6 and  7, the rates and PSNR of the images reconstructed from different layers are plotted. In these figures, the PSNRs shown in the legend box are for the full resolution layer and each curve in one color shows at that particular (full resolution) PSNR, the rates and PSNRs of images reconstructed from level 0, 1, 2,and 3 respectively.
   
   
   
   Fig. 6. The rate-distortion curve for image reconstructed from different layers and with different bit rates, critically sampled.
   
   
   

   Fig. 7. The rate-distortion curve for image reconstructed from different layers and with different bit rates, over sampled.
   
   

   
   To achieve the same full resolution PSNR, the oversampled pyramid requires more bits, as can be observed in the above figures and also from Fig. 5. Despite of this, due to the better subject quality of the image it provides, oversampled pyramid is still considered more suitable for providing better scalability at low rates.
   

   
   

   
   

---

Implementation Issues

1. Number of layers
   
   In the implementation, one parameter to choose is how many levels of scalability to use in pyramid coding. For subband coding, the more subbands we divide the image into, the flatter the spectrum is in each subband, which results in higher compression efficiency.  This is manifested in Fig. 6. More subbands give more flexibility in reconstructing images from lower layers as well.
   
   However, as the number of levels increases, the complexity also increases. There is a tradeoff in choosing a reasonable number of levels which also results in good compression performance. One can observe from Fig. 6 that,for subband decomposition, once we have three or more than three levels, the difference in performance is quite small. For this reason, we use three levels for critically sampled pyramid coding in our simulations.
   
   
   
   
   Fig. 8. R-D performance by using different number of levels, critically sampled.
   
   
   On contrary to the critically sampled pyramid, the R-D performance decreases as the number of levels goes up for the oversampled pyramid, as is shown in Fig. 9. This is because we have to encode more samples than those in the original image. In order to achieve good compression efficiency and make the comparison parallel to the critically sampled case (same number of multiresolution images), we use four layers for the oversampled scheme.
   
   
   
   
   Fig. 9. R-D performance by using different number of levels, oversampled.
   
   
   
2. Quantization
   
   For critically sampled pyramid, we use independent quantization of the subbands since the filters decorrelate the bands to a large extend. Because entropy coding is used after quantization, uniform quantizers are nearly optimal [5]. We choose the uniform scalar quantizer over the Loyd quantizer due to its simplicity and much lower complexity. We also performed an experiment of using both uniform and Loyd quantizers for subband images with greedy bit allocation algorithm. The R-D performance resulting from the two quantizers is compared in Fig. 10. We can observe that the difference is quite small, especially for higher bit rates.
   
   
   
   
   Fig. 10. Performance comparison of different quantizers.
   
   
   It is also discussed in [2] that vector quantization (VQ) is not usually not used for subbands since the pixels have little dependence and the complexity of VQ is not worthwhile. In order to make parallel comparisons, we also use the uniform quantizer in oversampled case as well.
   
   
3. Entropy coding
   
   Entropy coding is used to code quantized samples or groups of samples to achieve the maximum compression efficiency. Since coding schemes are not the focus of this work, we use entropy to represent the achievable bit rate, assuming the theoretical entropy bound can be approached closely enough by using suitable codes.
   
   Here we simply implemented a Huffman coder to compare the difference between entropy and bit rate achieved by Huffman coding. We know that Huffman codes are only within one bit of the true entropy [6]. Fig. 11 shows the comparison of entropy and rates by Huffman coder in coding the 10-subband decomposed images with the greedy bit allocation algorithm. It is observed that the rates by Huffman are very close to the true entropy, particularly at high rates. In lower rates, Huffman code is not that efficient for small alphabets, and in the worst case in our example Huffman code has to spend 0.2 more bit to achieve the same PSNR .
   
   
   
   
   Fig. 11. Entropy vs. rates achieved by Huffman coding.
   
   
   To further approach the entropy bound, better codes are available, such as vector Huffman coding [5] and run-length coding [6].
   

---

Conclusion

In this project, by comparing two pyramid coding schemes, we find that the critically sampled pyramid ourperforms the over-complete pyramid in terms of the rate-distortion performance due to the oversampling in the latter scheme.

Several papers [2][4] mention that better coarser versions in closed-loop pyramids can be achieved in terms of subjective quality, because of more freedom in choosing the decimation and interpolation filters. In our simulations, with a fixed PSNR in the full resolution, lower resolution images reconstructed from the open-loop pyramids have shown better subjective quality than those obtained from critically sampled subband pyramids. The over-complete pyramids are more suitable for low bit-rate coding in providing good subjective quality of coarse pictures. Another advantage of over-complete pyramid coding is its lower complexity, since it uses fewer quantizers in achieving the same number of layers of multiresolution. Other features of over-complete pyramid include control of quantization noise, and robustness counterbalance the oversampling problem [2].

Appendix: Work Distribution

References