The Influence of DCT Block Size on Coding Efficiency
An Adaptive Variable Block Size
Transform Coding System with Lagrangian Cost Function Decision Criterion
Submitted by Ayodele Embry
EE 368B
December 1, 2000
Abstract
The variable
block size coding technique has been proven to enhance performance over a fixed
transform coding system. However, there
are many different criterion which can be used to determine the optimal block
size. In this paper, the Lagrangian
cost function is proposed as that decision criterion. The results of the variable block size transform coding system using
the Lagrangian cost function as a decision criterion is compared with a rate
decision criterion, a distortion decision criterion and two static block size
transforms. In most cases, the
Lagrangian cost criterion outperforms all others.
Introduction
Transform
coding as been used extensively for efficient image compression. A typical transform coding system divides an
input image into fixed block sizes, usually of 8x8 or 16x16 pixels. At the transmitter, each block is
transformed by an orthogonal transform, usually the discrete cosine transform
because of its high-energy compaction and fast algorithms. The transform coefficients are then
quantized and coded for transmission.
At the receiver, the steps are reversed to produce the new image.
Many
image standards of the past have relied on a fixed block size for computing the
DCT. However, adaptive variable block size transform coding techniques have
proven to be capable of enhancing performance over fixed size transform coding
systems. A fixed block size cannot take advantage of the inconsistencies among
image statistics from one block to the next.
Large, uniform areas benefit more from the coarse granularity of a 16x16
block while areas of high detail and a high number of contrast edges would
benefit from a smaller block size to improve visual quality. To maximize the transform efficiency of an
image or group of images, the transform should adapt to the internal statistics
of the block to give a better tradeoff between bit rate and quality. There are several parameters which can be
made adaptive to an image including quantizer step size, bits allocated,
transform kernel and block size. Here,
we discuss adaptive block size as a method of maximizing the efficiency of the
DCT.
Variable Block Size Transform Coding Technique
In
the variable block size coding techniques used in [1] and [4], an image is
first divided into 16x16 blocks. Then each
of these blocks is subdivided into four 8x8 quadrants. A decision criterion is applied to see if
each quadrant should be encoded as four independent 4x4 blocks or as a single
8x8 block. If all four quadrants can be
encoded as 8x8 blocks, the criterion is applied to see if they can be further
merged and encoded as one 16x16 block.
Each block is then transformed by a DCT of corresponding size. Then quantization and coefficient coding are
applied to obtain the compressed data.
Figure 1 shows the order of quadrants in a 2Nx2N block of pixels.
To
reconstruct the original image, the decoding algorithm has to know the size of
each block it receives. In order to
achieve this end, a hierarchical data structure called a quadtree [3] is
used. A quadtree is a method of image
encoding using a simple tree structure.
Two representations of a quadtree are shown in Figure 2. The primary characteristic of this tree is
that each node of the tree has up to 4 children (none, if it is a leaf). In the variable block size transform
coding system described here, each node of the quadtree represents a block. If the block can be split into four quadrants,
then the node will generate four children nodes. Otherwise the node becomes a leaf.
Each
16x16 block of pixels in the image has its own quadtree. There are three levels in the quadtree with
the highest level, the root, representing the 16x16 block and the leaves in the
lowest tier representing 4x4 blocks. A one
is assigned to each non-leaf node and a zero to each leaf node. This quadtree code is sent along with each
block to assist the decoder in identifying the variable block sizes used for
each 16x16 group of pixels.
Many
quadtree representations use two bits to represent each quadrant. However, since this quadtree only contains
three levels, a variable length quadtree code is used. The maximum code length used for each 16x16
block is 5 bits. The first bit
represents whether or not the 16x16 block has been split. A zero is assigned if it has not been split,
a one if it has been. The next four
bits represent the four 8x8 quadrants of the 16x16 block. If any of these quadrants has been further
split into four 4x4 blocks, it is also given a one in the code, otherwise it is
assigned a zero. Figure 3 shows how the
quadtree code is formed while Figure 4 provides examples of quadtree encoding
for several different representations of a 16x16 block of pixels.
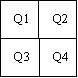
Figure 1: Quadtree segmentation into four quadrants

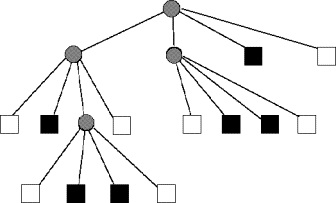
Figure 2: Quadtree representations
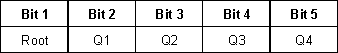
Figure 3: 5-bit binary quadtree code
A.  B.
B.  C.
C. 
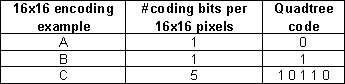
Figure 4: Sample quadtree coding of A) 16x16 block B) 16x16 block split into four 8x8 blocks
C) 16x16 block split into 4 8x8 blocks with 2 split further into 4x4 blocks
The Lagrangian
Cost Function
A
factor that contributes to the success of an adaptive variable block size
transform coding scheme is the choice of the decision criterion. A good criterion should determine whether or
not blocks should be merged or split to minimize the bit rate and maximize the
image quality. Ideally, if a 2Nx2N
block contains only smooth change and no high contrast edges, the blocks should
be merged. Otherwise, the blocks should
be split into four NxN blocks, each of which should have lower activity and
hence can be encoded more efficiently.
There
have been many suggested decision criteria for an adaptive variable block sized
DCT. In Chen's [1] system, a mean
difference based criterion is used on four adjacent blocks was proposed. This is essentially a distortion decision
criterion which uses the MSE as a measure.
In [4], See and Cham propose using an Edge
Discriminator as the decision criterion to reduce the number of high contrast
edges in a single block.
Here, we propose using the Lagrangian cost function to determine the optimal block size for an adaptive variable block size DCT. The Lagrangian cost function is an unconstrained cost function that helps to avoid unwieldy constrained optimization problems. It recognizes that for optimal image coding, it is important to balance both bit rate and image quality. The cost is determined by a linear function of the mean distortion and the rate scaled by a value, lambda. Choosing the appropriate value for lambda is important and is determined by simulation results. Figure 5 gives the equations for finding the Lagrangian cost function .
To find the optimal block size, the per pixel cost functions for different block sizes are compared. Whether or not the block is encoded as a single block or split into multiple smaller blocks is determined by the minimum cost function for that 16x16 block. Ideally, a lambda should be chosen that consistently gives a cost function decision criterion that provides the lowest possible bit rate and highest possible image quality.
A. J = D + lR
B. D =
E{(d(x,y)} where
d(x,y) = ||x - y||2
y = DCT coefficients
x = quantized DCT
coefficients
C. R =
E{length of codeword}
Figure 5: A) Lagrangian Cost Function B)
Average Distortion C) Bit Rate
In
order to determine the optimal DCT block sizes for the cost decision criterion,
the following steps are taken:
1)
Compare
the cost per pixel for the 16x16 block with the cost per pixel for the four
adjacent 8x8 quadrants. If the 16x16
block has a higher cost than the 8x8 blocks, split the 16x16 block into four 8x8
quadrants.
2)
For
each 8x8 block, compare the per pixel cost for the 8x8 block with the cost per
pixel for the four 4x4 quadrants of that block. If the 8x8 block has a higher
cost than the 4x4 blocks, split the 8x8 block into four 4x4 quadrants.
3)
Store
the quadtree code for that block.
4)
Take
the DCT using the appropriate block sizes as indicted by the quadtree code.
5)
Quantize
the DCT coefficients and transmit.
The
same steps are also taken to find the optimal variable block size DCT with the
rate and distortion decision criterions, replacing cost with the appropriate
measure.
Simulation Results
This
adaptive variable block sized transform coder is simulated using Matlab. The input image has a resolution of 8 bits
per pixel and the image size is 512x512 pixels. The three decision criterions used are the Lagrangian cost
function, average distortion, and bit rate.
All are determined on a per pixel average for a block. For comparison, static block size transform
coding is also performed with 8x8 and 16x16 block sizes.
For
the cost decision criterion simulations, seven values of lambda (0, 5, 10, 30,
62, 70, 90) are applied to the variable block size decision algorithm. For each decision criterion and static
block size, six quantizer step sizes (1, 2, 4, 8, 16, 32) were applied to
indicate any impact that the quantizer step size can have on the determination
of lambda or the relative performance of the five versions.
Figures
6 to 9 show the simulation results using two images, PEPPERS and BOATS. While the absolute values differ, both
images behave in the same manner for all measurements. Therefore, results will be discussed
collectively. Results are provided for
each decision criterion and both static block sizes.
6A)
6B)
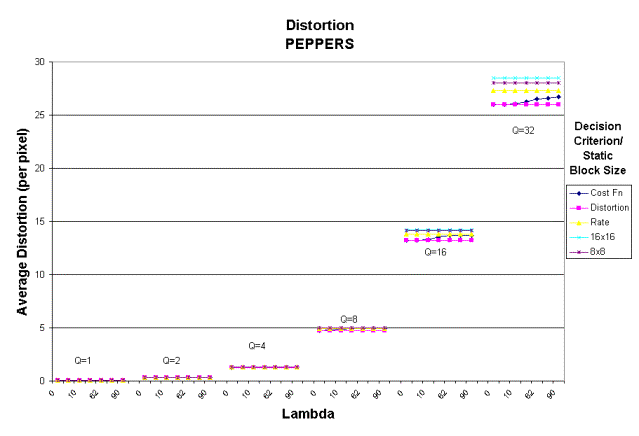
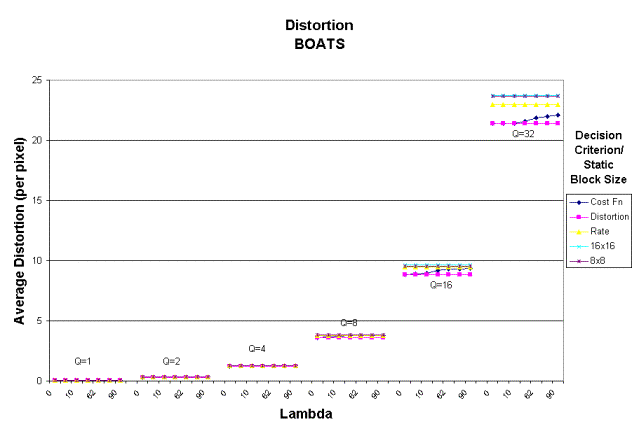
Figure 6: Average distortion per pixel for cost,
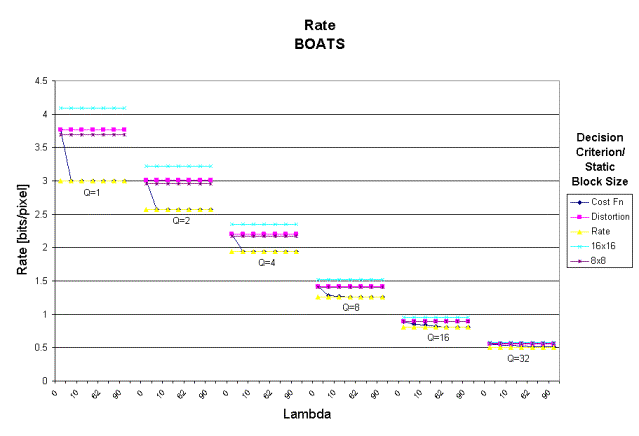
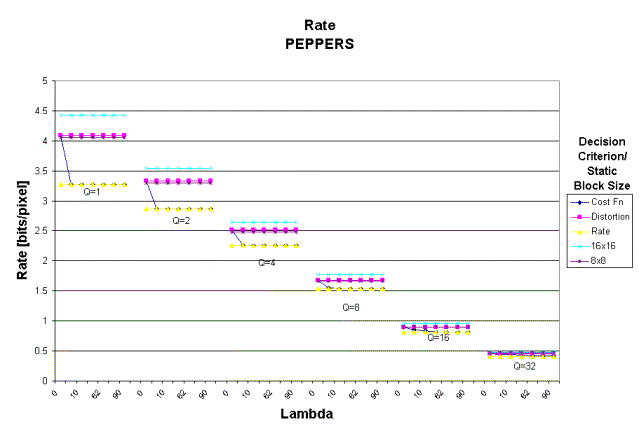
rate and distortion decision criterion and static block sizes of 8x8 and 16x16 for A) BOATS and B) PEPPERS.
7A)
7B)
Figure 7: Average bit rate per
pixel for cost, rate and distortion decision criterion and static block sizes
of 8x8 and 16x16 for A) BOATS and B) PEPPERS.
8A)
8B)
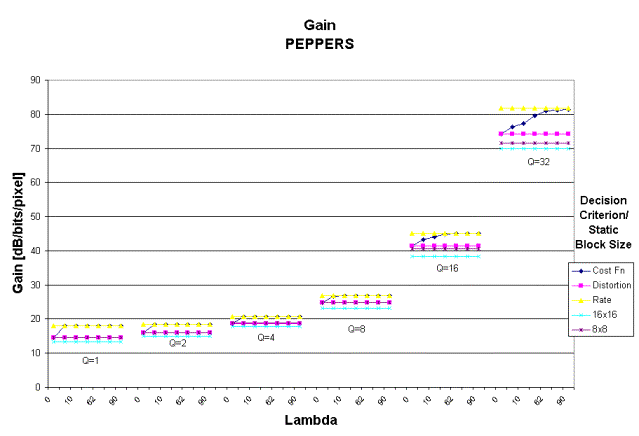
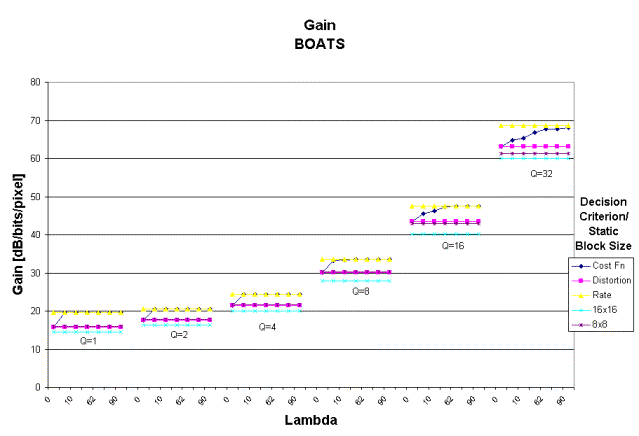
Figure 8: Gain measured as PSNR/Rate per pixel for cost, rate and distortion decision criterion and static block sizes of 8x8 and 16x16 for A) BOATS and B) PEPPERS.
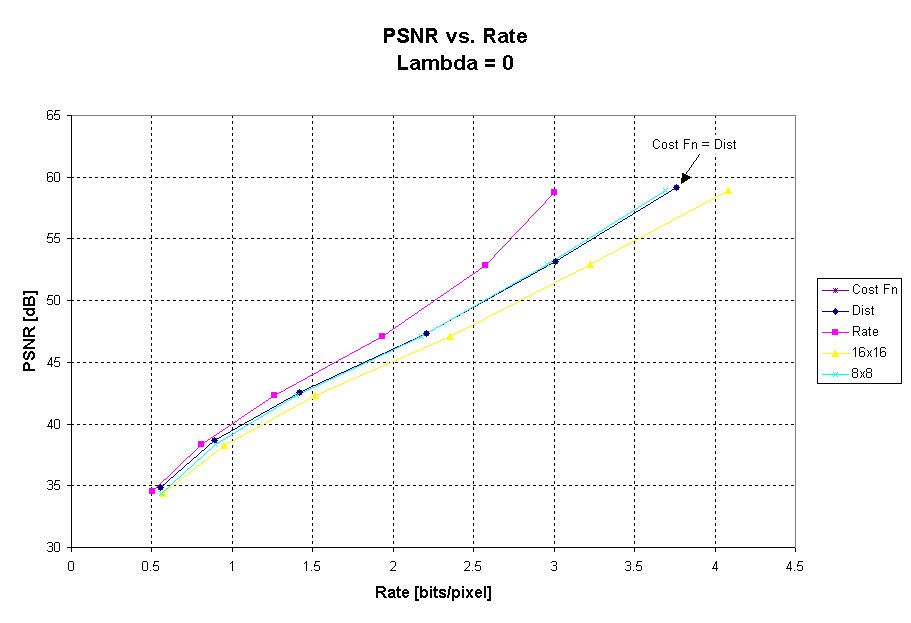
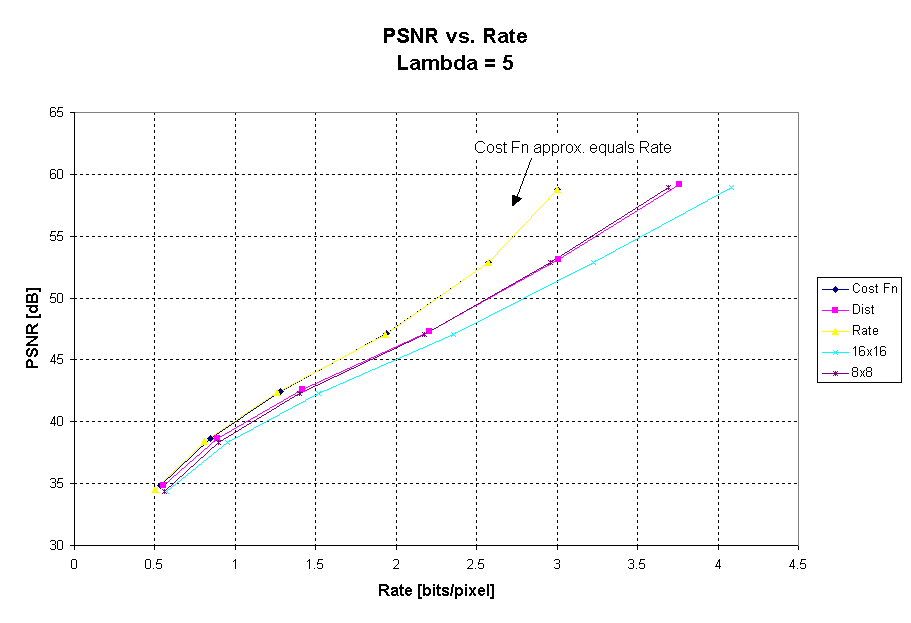
Figure 9: PSNR vs. Bit Rate
for cost, rate and distortion decision criterion and static block sizes
of 8x8 and 16x16 for BOATS.
Distortion Performance
Figure
6 shows the average distortion per pixel measured for PEPPERS and BOATS. For small quantizer step sizes (Q = 1, 2,
4,8), using the Lagrangian cost function as a decision criteria for adaptive
variable block size DCT results in an overall per pixel image distortion
slightly lower than either the static 8x8 or 16x16 block size. At larger quantizer step sizes (Q = 16, 32),
using the cost criterion results in a significant improvement in the average
distortion. When comparing the cost criterion with the results for the
distortion and rate criterion, the cost function performs almost as well as
using distortion only as a criterion for small quantizer step sizes. For larger quantizer step sizes, lambda
should be below 10 to minimize distortion.
Bit Rate Performance
Using
the Lagrangian cost function as a decision criterion lowers the average bit
rate per pixel over using a static block size for all quantizer step sizes as
shown in Figure 7. For a quantizer step
size of one, the bit rate is more than
one bit per pixel less than a static 16x16 block and almost 0.7 bits less than a
static 8x8 block with a quantizer step size of one. As the quantizer step size increases, the difference diminishes,
but is still noticeable. The cost
criterion performs as well as the bit rate decision criterion for small
quantizer step sizes as long as lambda is greater than zero. For larger step sizes, cost performs almost
as well as the rate for lambda greater than 5.
Gain
The
relative gain is determined by dividing the PSNR by the per pixel bit rate for
a particular lambda and quantizer step size. This gain indicates the relative
improvement in both bit rate and image quality that provides the most efficient
compression. With the exception of
lambda equal to zero for small quantizer step sizes, using the cost decision
criterion gives better performance than a static block size of 8x8 or 16x16. Increasing lambda beyond 5 gives no
improvement for these small step sizes.
However, for quantizer step sizes of 16 and 32, increasing lambda amplifies
the gain. This gain begins to level out
once lambda equals 30. The cost
criterion provides a higher gain than the distortion criterion for all lambda
greater than five and matches or exceeds the gain for a rate decision criterion
at small quantizer step sizes. At
large quantizer step sizes, the gain for the cost criterion lags that of the
rate criterion for small lambda (less than 30).
PSNR vs. Rate
Figure 9 gives the PSNR vs. Rate graph for BOATS. For lambda equal to zero, we see that the cost function almost exactly equals that for using the distortion only as a decision criterion. This is expected since rate is not being taking into account as part of the decision criterion. At lambda equal to zero, the rate performs much better than any of the other methods. For all lambda greater than zero, the results using the cost function decision criterion almost exactly equal the results using the rate as the decision criterion. Using the rate or cost as a decision criterion gives a gain of almost 7dB at high bitrates. At very low bitrates, a gain of almost 1dB can be achieved.
Conclusion
From these simulation results, it can be seen that using the Lagrangian cost function as a decision criterion for adaptive variable block size transform coding produces lower bit rates and higher image quality when compared to a static block size. Using a Lagrangian cost function decision criterion achieves performance which exceeds that of using only a distortion criterion by up to 7dB at high bitrates and close to 1dB at low bitrates . From these simulations, it can be seen that an optimal lambda should be greater than zero to obtain the maximum gain.
Bibliography
[1] C-T CHEN, 'Adaptive Transform Coding Via
Quadtree-Based Variable Blocksize DCT', International
Conference on ASSP, pp. 1854-1857, 1989.
[2] M.H. LEE and G. GREBBIN, 'Classified vector
quantization with variable block-size DCT models', IEE Procedures on Visual Image Signal Processing, Vol. 141, No. 1,
February 1994.
[3] H. SAMET, ‘The quadtree and related
hierarchical data structures', ACM
Computing Surveys, pp. 188-216, 1984.
[4] C-T SEE and W-K CHAM, 'An Adaptive Variable
Block Size DCT Transform Coding System', International
Conference on Circuits and Systems, June 1991.