Research Discussions

The following log contains entries starting several months prior to the first day of class, involving colleagues at Brown, Google and Stanford, invited speakers, collaborators, and technical consultants. Each entry contains a mix of technical notes, references and short tutorials on background topics that students may find useful during the course. Entries after the start of class include notes on class discussions, technical supplements and additional references. The entries are listed in reverse chronological order with a bibliography and footnotes at the end.

May 11, 2017

Stephen Plaza in collaboration with Shinya Takemura and their collaborators at HHMI Janelia Farm Research Campus run the FlyEM Project. Stephen sent us an early draft of the Drosophila Mushroom Body Dataset available to students taking CS379C interested in structural connectomics projects or combined structural and functional alignment. Regarding the draft data, Stephen writes, "To clarify, the dataset is complete in terms of neuron morphology and connectivity detail. It is only missing the grayscale and near pixel perfect segmentation of neurons."

For those of you familiar with Drosophila Seven-Column Medulla dataset, Stephen notes that "You will [need → "meet" or "find"] interesting motifs (that are not in the optic lobe) with multiple KC [Kenyon Cell] neurons synapsing at the same location of an MBON [Mushroom Body Output Neuron] dendrite. We often call these sites convergent synapses. It appears that the KC is probably connecting to a neighboring KC and the MBON. It is possible that multiple KCs at the site need to be 'active' for the MBON to be active there."

Here are a few review papers that will introduce you to the mushroom body and related parts of the olfactory system: [9] PDF, [153] PDF, [21] PDF, [71] PDF, and [109] PDF and here is a snapshot of the Mushroom Body Dataset. The tar ball (TAR) includes json files containing Python dictionary data structures describing neurons, T-bar structures, and synapses as well as skeletons for all of the reconstructed neurons. For those of you familiar with the Seven-Column Medulla Dataset, the format is almost identical:

% du -h
 41M        ./mb6_skeletons_7abee
220M        .
pystat -v ./mb6_skeletons_7abee/ → 36,549,715 bytes (43.1 MB on disk) for 2,400 skeletons

% cat annotations-body_7abee_201705_11T234538.json | grep -i "body id" | wc -l → 2,434 neurons

% cat mb6_synapses_10062016_7abee_all.json | grep -i "T-bar" | wc -l → 91,443 T-bar structures

% cat mb6_synapses_10062016_7abee_all.json | grep -i "body id" | wc -l → 317,998 T-bar + synapses

% cat mb6_synapses_10062016_7abee_kc_roi_alpha.json | grep -i "T-bar" | wc -l → 13,664 T-bar structures

% cat mb6_synapses_10062016_7abee_kc_roi_alpha.json | grep -i "body id" | wc -l → 48,210 T-bar + synapses 

@article{AsoetallELIFE-14,
       author = {Aso, Y. and Hattori, D. and Yu, Y. and Johnston, R. M. and Iyer, N. A. and Ngo, T. T. and Dionne, H. and Abbott, L. F. and Axel, R. and Tanimoto, H.  nd Rubin, G. M.},
        title = {The neuronal architecture of the mushroom body provides a logic for associative learning},
      journal = {Elife},
       volume = {3},
         year = {2014},
        pages = {e04577},
     abstract = {We identified the neurons comprising the Drosophila mushroom body (MB), an associative center in invertebrate brains, and provide a comprehensive map describing their potential connections. Each of the 21 MB output neuron (MBON) types elaborates segregated dendritic arbors along the parallel axons of approximately 2000 Kenyon cells, forming 15 compartments that collectively tile the MB lobes. MBON axons project to five discrete neuropils outside of the MB and three MBON types form a feedforward network in the lobes. Each of the 20 dopaminergic neuron (DAN) types projects axons to one, or at most two, of the MBON compartments. Convergence of DAN axons on compartmentalized Kenyon cell-MBON synapses creates a highly ordered unit that can support learning to impose valence on sensory representations. The elucidation of the complement of neurons of the MB provides a comprehensive anatomical substrate from which one can infer a functional logic of associative olfactory learning and memory.}
}
@article{ShaoetalTBE-14,
       author = {H. C. Shao and C. C. Wu and G. Y. Chen and H. M. Chang and A. S. Chiang and Y. C. Chen},
        title = {Developing a Stereotypical Drosophila Brain Atlas},
      journal = {{IEEE Transactions on Biomedical Engineering}},
       volume = {61},
       number = {12},
         year = {2014},
        pages = {2848-2858},
     abstract = {Brain research requires a standardized brain atlas to describe both the variance and invariance in brain anatomy and neuron connectivity. In this study, we propose a system to construct a standardized 3D Drosophila brain atlas by integrating labeled images from different preparations. The 3D fly brain atlas consists of standardized anatomical global and local reference models, e.g., the inner and external brain surfaces and the mushroom body. The averaged global and local reference models are generated by the model averaging procedure, and then the standard Drosophila brain atlas can be compiled by transferring the averaged neuropil models into the averaged brain surface models. The main contribution and novelty of our study is to determine the average 3D brain shape based on the isosurface suggested by the zero-crossings of a 3D accumulative signed distance map. Consequently, in contrast with previous approaches that also aim to construct a stereotypical brain model based on the probability map and a user-specified probability threshold, our method is more robust and thus capable to yield more objective and accurate results. Moreover, the obtained 3D average shape is useful for defining brain coordinate systems and will be able to provide boundary conditions for volume registration methods in the future. This method is distinguishable from those focusing on 2D + Z image volumes because its pipeline is designed to process 3D mesh surface models of Drosophila brains.},
}
@article{CampbellandTurnerCURRENT-BIOLOGY-10,
       author = {Robert A.A. Campbell and Glenn C. Turner},
        title = {The mushroom body},
      journal = {Current Biology},
       volume = {20},
       number = {1},
        pages = {R11-R12},
         year = {2010},
     abstract = {The mushroom body is a prominent and striking structure in the brain of several invertebrates, mainly arthropods. It is found in insects, scorpions, spiders, and even segmented worms. With its long stalk crowned with a cap of cell bodies, a GFP-labeled mushroom body certainly lives up to its name (Figure 1). The mushroom body is composed of small neurons known as Kenyon cells, named after Frederick Kenyon, who first applied the Golgi staining technique to the insect brain. The honey bee brain, for instance, contains roughly 175,000 neurons per mushroom body while the brain of the smaller fruit fly Drosophila melanogaster only possesses about 2,500. Kenyon cells thus make up 20\% and 2\%, respectively, of the total number of neurons in each insect’s brain. Kenyon cell bodies sit atop the calyx, a tangled zone of synapses representing the site of sensory input. Projecting away from the calyx is the stalk comprised of Kenyon cell axons carrying information away to the output lobes. }
}
@article{HeisenbergNATURE-REVIEWS-NEUROSCIENCE-03,
       author = {Heisenberg, M.},
        title = {Mushroom body memoir: from maps to models},
      journal = {Nature Reviews Neuroscience},
       volume = {4},
       number = {4},
         year = {2003},
        pages = {266-275},
     abstract = {Genetic intervention in the fly Drosophila melanogaster has provided strong evidence that the mushroom bodies of the insect brain act as the seat of a memory trace for odours. This localization gives the mushroom bodies a place in a network model of olfactory memory that is based on the functional anatomy of the olfactory system. In the model, complex odour mixtures are assumed to be represented by activated sets of intrinsic mushroom body neurons. Conditioning renders an extrinsic mushroom-body output neuron specifically responsive to such a set. Mushroom bodies have a second, less understood function in the organization of the motor output. The development of a circuit model that also addresses this function might allow the mushroom bodies to throw light on the basic operating principles of the brain.},
}
@article{McGuireetalSCIENCE-01,
       author = {McGuire, S. E. and Le, P. T. and Davis, R. L.},
        title = {The role of {D}rosophila mushroom body signaling in olfactory memory},
      journal = {Science},
       volume = {293},
       number = {5533},
         year = {2001},
        pages = {1330-1333},
     abstract = {The mushroom bodies of the Drosophila brain are important for olfactory learning and memory. To investigate the requirement for mushroom body signaling during the different phases of memory processing, we transiently inactivated neurotransmission through this region of the brain by expressing a temperature-sensitive allele of the shibire dynamin guanosine triphosphatase, which is required for synaptic transmission. Inactivation of mushroom body signaling through alpha/beta neurons during different phases of memory processing revealed a requirement for mushroom body signaling during memory retrieval, but not during acquisition or consolidation.}
}

May 5, 2017

Data Alignment Problems

Despite the claim of its being a full reconstruction, most cell bodies in the seven-column data are not included. Technically, the claim is valid, since in most cases the cell bodies are not even in the medulla. Stephen Plaza said this is due to a limitation of earlier FIBSEM technology, and, while the problem does not arise in aligning the whole fly brain connectome, it undermines our original idea of aligning the known locations of cell bodies in the EM data with the 2PE emissions / putative cell-body locations in the calcium imaging data. However, while we don't know the locations of most cell bodies, we do know most of the structure of the axonal and dendritic arbors as well as location of most if not all the locations of synapses arranged on the T-bar structures typical of most fly neurons. Unfortunately, the synapses do not express the fluorescent calcium indicators, indeed it would seem we might expect very little in terms of fluorescent excitation within the medulla proper.

Figure 1:  This slide shows a cloud of points that reveal the outlines of seven neurons called type-one medullary intrinsic neurons or Mi1 for short. The points of the central column Mi1 are blue, and those of the surrounding six Mi1 neurons are shaded green. I’ve fit a line to each neuron: red for the central-column Mi1 and yellow lines for the adjacent Mi1 neurons. The data is from the HHMI Janelia Research Campus FlyEM Project.

Stephen and Shinya Takemura suggested that, since neurons are identified by their cell types (Tm, Dm, Mi, etc) and their position and morphology is significantly stereotyped, we could use full reconstructions found in the literature to predict exactly where their cell bodies would lie just outside or within the tracts / bundles around the periphery of the medulla1. Alternatively, depending on the type of microscopy employed for calcium imaging, e.g., some variant of confocal microscopy could work, we might be able to construct a distinctive pattern using the full skeletons of those neurons, e.g., Mi1 and Tm1, whose processes are entirely contained within the columns of the medullar neuropil—see Figure 1.

By using the skeletons to register the seven column data, we would not immediately have the aligned cell bodies, but we would be in a much better position to estimate their position, making additional changes to the alignment in order to find the best alignment with the functional data. Just to be clear matching a pattern constructed from the full skeletons of column bound neurons would have to be done relying upon confocal imagery alone; I am presuming the imagery data could be acquired prior to running the experimental protocol and recording the florescent proxy for the calcium flux.

Figure 2:  A 3D mesh—rendered here using MeshLab—reconstruction of the Drosophila half brain employed by the Insect Brain Name Working Group in developing a hierarchical nomenclature system for the major brain regions and fiber bundles found in insect brains, using the brain of Drosophila melanogaster as the reference framework. This nomenclature is intended to serve as a standard of reference for the study of the brains of Drosophila and other insects [81]. The region shaded pink in the above graphic corresponds to the medulla.

Fly Datasets and Tools

We've been working with two lower-resolution datasets to facilitate registration: the Adult Drosophila Brain (2010) from the HHMI Janelia Farm Research Campus (JFRC) and the Adult Drosophila Half Brain (2014) from the Insect Brain Name Working Group (IBNWG) —see Figure 2. Both datasets include image stacks, 3D mesh templates, and image masks for 50 neuropil domains including medulla.

For analysis and visualization, we're using a number of tools including: Vaa3D from JFRC and the Allen Institute for Brain Science (AIBS), ImageJ from NIH, open-source tools for working with points clouds CloudCompare and 3D mesh models MeshLab, and a Python library NeuroBot for working with the JFRC Seven-Column Medulla dataset [CODE].

Alignment Algorithms

Here is a first pass at an algorithm for aligning the functional and structural datasets, taking into account the issues raised above: The first step is to construct a morphologically-unique 3D pattern using structural features from the JFRC dataset, for example, by using the skeletons of columnar-bound intrinsic neurons fully contained within the medulla (Figure 1), in order to identify the location and orientation of the corresponding seven columns in Sophie's data. The pattern is basically a 3D binary image that we match against 3D whole or half-brain image—an image of just the medullar neuropil is sufficient—generated using a light source with a broader spectrum than the fluorescent excitation light and perhaps a different microscope than the epifluorescence microscope used to acquire the calcium imagery2.

Once we know the location of the seven columns in Sophie's fly data, we need to identify the cell bodies of the neurons whose processes are represented / largely contained within the seven-column volume. Given that most if not all of the these cell bodies will be located outside the seven-column volume, we need to extend this volume to include the extra-medullar regions likely to contain these cell bodies. Having identified a minimal volume V in which to search for the cell bodies of medullar neurons, we need to construct a dataset corresponding to a 3D V-shaped slice out of the calcium indicator time-series recordings.

Figure 3:  The upper green rectangle with the inset reddish-hued 2PE image slice—rendered here using Fiji—is superimposed on a cross-section of the IBNWG half-brain—rendered using Vaa3D, and represents the approximate location of the functional data that Sophie Aimon sent us in April. For the purpose of aligning the JFRC seven-column data with the medulla, we need functional data from the region roughly corresponding to lower green rectangle.

Figure 3 shows the approximate location of the region of adult fly brain that was imaged in the data that Sophie sent us in April—see the inset reddish-hued 2PE image slice in the upper green rectangle shown in Figure 3. For our present purposes, we need functional data from the region roughly corresponding to lower green rectangle in Figure 3. We also need 3D light imagery of the region for the purpose of alignment.

Finally, we should think about how we can verify that we have correctly aligned the seven columns with the functional recordings. For one thing, we know from Shinya Takemura [171, 172] that the tissue corresponding to the seven-column data was approximately from the center of the visual field. We will be able to check on this in silico using the reference frame provided by the Ito et al [81] data. In addition, Art Pope and I discussed various experimental stimuli3 and fiducial labeling strategies4 that might help us to determine whether we have correctly identify the seven-column sub volume.

Functional Analyses

There are a number of ways in which we could succeed in this endeavor and related ways in which we could capitalize on our success—all of them listed here assume some success in matching the seven-column-pattern to some location and orientation in the medulla that satisfies the centrality constraint and bears up under visual scrutiny:

  1. We (a) obtain one stand-out match and (b) succeed in lining up the corresponding extra-medullar cell bodies.

  2. We obtain multiple matches with approximately the same score, and achieve (b) for each one of these matches.

  3. We (a) obtain one stand-out match but (b) we fail in lining up the corresponding extra-medullar cell bodies.

Case #1 is the ideal case and it provides the opportunity to generate time series of transmission-response matrices [37] and perform analyses using tools from graph-theory, e.g., spectral methods [113], and algebraic topology, e.g., persistent homology [26, 99]. In Case #2, we can treat the seven-column pattern as a motif finder [85, 179, 74, 96, 97] that can be used to statistically analyze the corresponding collocated functional and structural domains, even though we can't map fluorescent emissions directly to nodes (neurons) in the connectome graph.

Case #3 offers the opportunity to apply unsupervised machine learning methods to automatically sort out the connections by using the connectome graph, the functional data and a set of proposals for mapping fluorescent emissions to nodes in the connectome graph. Basically, we assign each cell body in the seven-column structural data a set of candidate locations in the functional data and then train a network with a loss function that measures how well different assignments predict the next neural state vector. I realize these descriptions are too brief to be of much use to anyone who can't read my mind, but perhaps they'll motivate you to start thinking about what sort of science we can enable in this project.

April 27, 2017

A few observations and suggestions concerning the problem of aligning functional and structural data. First, our basic task is to fit a point cloud corresponding to the coordinates of the non-zero voxels in some thresholded version of Sophie's data to the mesh, i.e., find the orientation and scaling parameters that "optimally" enclose this point cloud. Once we have that we can use the medulla model to identify all putative neurons in the medulla and construct a point cloud for these neurons that we can use to find correspondences with the seven-column cell bodies. Here are some notes relating to implementation5:

  1. I was able to use a 2008 MacPro server with 8GB and 8 cores to run ImageJ and allocated 7GB to the application. It eventually ran out of memory on even the smallest of Sophie's datasets, but basically did fine for viewing for long enough to be useful before it froze;

  2. The raw video shows the outlines of the (outer surface of the) brain tissue, well enough that we can probably get some accurate initialization alignment points to make it easier to fit the data;

  3. I found that the preprocessed video is best viewed by applying the 16 Color LUT — click the >> icon on the far right hand side of the tools menu, and select LUT which will put the LUT options sub menu on the main tools menu;

  4. In this mode, you should see a lot of activity as you move through the center of the stack. In my case, most of the screen was light blue, the majority of cell bodies yellow but with a few other colors.

  5. I am using MeshLab for viewing mesh models and CloudCompare for point clouds. Thanks to Art for pointing out these tools as they are — for the most part — professionally engineered tools that scale to accommodate large datasets;

  6. There are a bunch YouTube videos showing how to use these tools to register / align point clouds and mesh models. One problem I anticipate involves registering a point cloud in which the points (a) reside in the interior as well as on the surface, and (b) are sparse and don't represent a random sample ... indeed, they very sparse in some peripheral areas of the brain. It may be possible to segment out the coronal cross sections of the brain well enough to define the exterior surface and then densely sample points on each such cross section to create a point cloud of the whole brain consisting of only points on the brain tissue surface;

  7. Given a point cloud of the sort described in item 6 it should be relatively easy register the cloud with the JFC [83] (Janelia Farm Campus) mesh model using an affine transformation. There are also tools that can compute non-affine transformations to handle non-uniform deformations. This may be overkill if we use physics-based deformable (spring) models to estimate different possible alignments. Fortunately, Art knows a lot about this sort of problem and the existing algorithms and tools for solving them;

  8. I didn't look very hard but so far I haven't found a 3D mesh of the medulla, though Virtual Fly Brain — VFB_BRAIN and VFB_HALF_Brain — claims to have (or soon have) them. However, I did find a stack of annotated coronal-cross-sectional images that clearly show the boundaries of the medulla and these masks directly map to the whole-brain mesh model I sent around earlier;

  9. Once we register the CI image point cloud with the JFC mesh model we should be able to use the same transformation on the stack of medulla-image masks to determine a point cloud consisting of just neurons residing within the medulla;

  10. The final step is to align the point cloud corresponding to the coordinates of the cell bodies in the seven-column dataset with the point cloud consisting of the CI identified medullar cell bodies;

April 25, 2017

You can get the general idea of what I expect for the final project proposals from the archived class web pages, but it's important to note that the content of the proposals depends very much on the topic for each year.

In 2013, the focus was on identifying technologies that would mature in 2, 5 and 10 years and that could fundamentally change how we do neuroscience:

Neuroscientists have by and large failed to take advantage of the exponential trend in computational power known as Moore’s Law. In this class, we investigate new approaches to scalable neuroscience that might enable systems neuroscience to exploit the accelerating returns from recent advances in sensing and computation.

Projects (see here) were in the form of a term paper:

Grading is based on a midterm white paper [the proposal] and a final technical report [the project] evaluating an appropriate technology selected in collaboration with the instructor. Examples include nanoscale networks, photo-acoustic microscopy, high-intensity focused ultrasound and computer-vision-based analysis of micrographs.

The results were combined into a jointly-authored arXiv paper describing our findings entitled On the Technology Prospects and Investment Opportunities for Scalable Neuroscience, available in HTML and PDF formats, that was published on arXiv, widely circulated in the community, and quite influential.

In 2012, the focus was on modeling neural systems and analyzing data:

This year students in CS379C will have the opportunity to interact with some of the most innovative scientists and engineers working in systems neuroscience today. We will study their methods and hear directly from them about the challenges they face, some of which the students can actually help out with now.

Projects (see here) were in the form of writing code and testing systems:

Projects will include replicating and evaluating existing computational models and implementing novel models that extend or combine the features of existing ones.

This year the focus is on learning models from large datasets:

This year's class focuses on inferring computational models from neural-recording data. Lectures, invited speakers and projects all emphasize functional rather than structural inference. [...] We will arrange access to large functional datasets along with tools for working with such datasets and suggestions for modeling methods and machine learning technologies for performing inference.

​​The class discussion​ includes a number of project ideas​ and I've mentioned others in class. I'm not a stickler for the exact format and I've taken pains not to stifle your creativity, but I expect you to make a best effort to align your interests with the focus spelled out in the course description and reiterated above. Here are some ideas that you should be able to expand into a 300-word​ pre-proposal:

  1. Use the new C. elegans BIORXIV 2017 data from Andrew ​Leifer's lab and apply the techniques that Saul Kato described to build and compare a dynamical systems model.

  2. Analyze the Kato CELL-2015 and Leifer PNAS-2016 data using a more powerful dimensionality reduction technique and compare to the original Kato model.

  3. Compare the mouse striate cortex resting state (no stimulus) activity in the Pachitariu data with the drosophila (no stimulus) activity in the Aimon data.

  4. Compare the mouse striate cortex resting state (no stimulus) activity in the Pachitariu data with activity in related cortical areas from the Allen Institute data.

  5. Replicate [a specified subset] of the results reported in the Ahrens NATURE-2012 or ELIFE-2016 papers ... and so on ...

... and so forth. These are just suggestions. Before you can expand any one of them into a 300 word pre-proposal, you'll have to read (or at least scan) the relevant papers (listed in the calendar entries of the above-mentioned authors ... Andy Leifer participated in class last year and so look at his entry in the 2016 calendar that you'll find in the course archives) and check out the relevant supplementary materials (which you'll find on along with the paper on the journal website).

The final version of your proposal will be due one week (Tuesday, May 9) after the pre-proposal is due.

April 23, 2017

There's a new paper from Andrew Leifer's lab on his most recent work on recording from C. elegans in freely moving nematode worms. See Nguyen et al PLoS Computational Biology (in press) 2017 [118] (PDF) and accompanying data and software tools Nguyen et al IEEE Dataport [119] (HTML). If you're interested in C. elegans, this paper and its associated supplements are worth a look.

Sophie Aimon has provided two datasets using the recording technology described in her 2015 bioRxiv paper [4]. Keep in mind that this data is lower resolution than the best recordings we have for zebrafish. Nonetheless it probably represents the current state of the art in whole-fly functional imaging. My colleagues, Peter Li and Art Pope at Google, are looking at the data to determine if alignment with the seven-column-medulla structural data from FlyEM is possible.

April 21, 2017

Subject: "Frustration is a matter of expectation", Luis von Ahn on the the value of "I don't understand":

My phD advisor at Carnegie Mellon was Manuel Blum, who many people consider the father of cryptography. He's amazing and he's very funny. I learned a lot from him. When I met him, which was like 15 years ago, I guess he was in his 60's, but he always acted way older than he actually was. He just acted as if he forgot everything.

I had to explain to him what I was working on, which at the time was CAPTCHA, these distorted characters that you have to type all over the Internet. It's very annoying. That was the thing I was working on and I had to explain it to him.

It was very funny, because usually I would start explaining something, and in the first sentence he would say, 'I don't understand what you're saying', and then I would try to find another way of saying it, and a whole hour would pass and I could not get past the first sentence. He would say, 'Well, the hour's over. Let's meet nest week.' This must have happened for months, and at some point I started thinking, 'I don't know why people think this guy's so smart.'

Later, I understood what he was doing. This is basically just an act. Essentially, I was being unclear about what I was saying, and I did not fully understand what I was trying to explain to him. He was just drilling deeper and deeper and deeper until I realized, every time, that there was actually something I didn't have clear in my mind. He really taught me to think deeply about things, and I think that's something I have not forgotten.

April 19, 2017

Five Suggested Topics for Final Class Projects in CS379C:

Topic #1: Dynamical System Modeling Nematode Caenorhabditis elegans:
Functional → Zimmer and Leifer Labs
Contacts: Saul Kato, Andrew Leifer (see here [Kato, 2016], here [Leifer 2016] and here [Leifer 2017])
Structural → Worm Atlas Hermaphrodite Connectome
Contacts: Saul Kato, UCSF, Semon Rezchikov, MIT

Topic #2: Structural and Functional Alignment Drosophila melanogaster:
Functional → Greenspan Lab
Contacts: Sophie Aimon, UCSD
Structural → HHMI Janelia FlyEM Project
Contacts: Stephen Plaza, HHMI, Shinya Takemura, HHMI

The medulla forms hexagonal columnar arrays: one center column with six neighbors. One can think of these columns as parallel units in a receptive field within a retinotopic map if flies had a retina.

There are several goals for analyzing seven adjacent medulla columns (SOURCE):

Shinya Takemura writes: "Below shows a medulla neuron Mi9 that stretches the entire medulla depth and has a cell body in the medulla distal surface. Our EM image stack spans these medulla cell body layers through the depth slightly deeper than the proximal edge of M10. I can search another cell type if it is useful to align it with the functional data. I can also provide multiple cells because we have reconstructed seven medulla columns. The cell body locations and the proximal edge of the medulla neuropil would be useful landmarks. The seven columns were imaged in the middle of retinotopic field, i.e. almost the middle of the medulla in both dorso-ventral and antero-posterior axes":

Functional imaging the brain using light field microscopy [4]. a) Experimental set up: The fly is head fixed and its tarsi (legs) are touching a ball. The light from the brain goes through the objective, the microscope tube lens, a microlens array, and relay lenses, onto the sensor of a high-speed sCMOS camera. The behavior is recorded with another camera in front of the fly. b) Example of a light field deconvolution. Top: 2D light field image acquired in 5 ms exposure with a 20 x objective. Bottom: Anterior and posterior views (slightly tilted sideways) of the computationally reconstructed volume. 3D bar is 90 x 30 x 30 µm. (SOURCE)

Topic: #3: Functional Modeling of Whole Zebrafish Brain Danio rerio:
Functional → Ahrens Lab
Contacts: Misha Ahrens, HHMI

Topic: #4: Functional Modeling of Mouse Visual Cortex Mus musculus:
Functional → Harris and Carandini Lab
Contact: Marius Pachitariu, UCL
Functional → Allen Institute Project MindScope
Contact: Michael Buice, AIBS

Topic: #5: Atari Game Console and 6502 Processor Computatus motorola:
Functional → 6502 Emulation
Structural → Virtual 6502
Contacts: Eric Jonas, UCB (see here)

April 17, 2017

There seems to be some confusion regarding the different types of microscopy discussed in the readings and used in collecting the datasets. Here's a quick comparison of the different technologies we'll be reading about that are employed for collecting functional data and you can find a concise compilation that covers a larger collection of technologies here:

So, for example, Ahrens et al [3] use light-sheet microscopy whereas Aimon et al [4] use light-field microscopy. Pachitariu et al [126] use an off-the-shelf resonant-scanning microscope but employ a novel pipeline for post-processing the raw image data7. Saul Kato and other researchers in Manuel Zimmer's lab use light-field microscopy and related imaging technology developed in Alipasha Vaziri's lab [135, 136, 134, 149].

The microlens arrays used in commercial light-field cameras such as those manufactured by Lytro mimic the structure of the insect compound eye such as the multi-faceted arthropod eye of the fly. However, light-field cameras also capture the direction of the light rays and hence collect more information than insect eyes. See Song et al [162] for the description of an engineered lens system that uses an array of 180 artificial ommatidia to achieve a 160-degree field of view.

April 15, 2017

Here is the first installment of sample projects that make use of the datasets mentioned in the April 11 entry in this log:

Aligning Functional and Structural Connectomic Data: (a) Identify the location of the seven columns in the Drosophila medulla accounted for in the dataset from Janelia [171]. (b) Align the whole-brain functional data [4] from Ralph Greenspan's lab with the columns of the Janelia data. (c) Use the aligned data to generate a times series of transmission-response graphs. (c) Apply graph-theoretical and topological algorithms to analyze the resulting time series.

Commentary: This is probably the closest we can come to creating an aligned functional and structural dataset at this time. When Janelia and Neuromancer complete the whole-fly connectome, the capability addressed in this project will realize its full potential. The project is challenging enough that it will require a small team of students to take on the alignment part. Fortunately, we will have help from two labs. Sophie has provided an initial sample of data and promises to collect more if we come up with some interesting results. Stephen Plaza and Shinya Takemura are helping to identify the location, shape and orientation of the sample tissue they used for the seven-column data.

As an incentive, Olaf Sporns, the editor of Network Neuroscience, has asked me to submit a manuscript describing the work I presented at the Keystone Symposium on Molecular and Cellular Biology in March, and, if successful in aligning the functional and structral data, I will be happy to add the members of the successful team to the list of co-authors on this paper.

Challenges: (i) The two datasets were collected from different phenotypes. The good news is that the fly optic lobe exhibits a good deal of stereotypy across phenotypes and is not known to exhibit plasticity, unlike the olfactory bulb and related mushroom bodies. The medulla is highly regular and so we hope to construct a pattern of points corresponding to the locations of the cell bodies in the seven-column connectome graph embedding, and then search for correspondences within the functional point cloud. (ii) The EM (structural) image data has voxels of size on the order of 10nm on a side, while the 2PE (functional) data has approximately 2μm resolution. The good news is we are trying to match fluorescent emissions from cell-body nuclei with known locations of specific neuron types in the seven-column data.

Applications of Algebraic Topology in Neuroscience: This is really a constellation of possible projects centered around the use of tools from algebraic topology to analyze structural and functional datasets. Here are a few representative papers organized roughly by topic: (i) introductory [33, 128], (ii) structural [37, 158, 56, 131], (iii) functional [28, 34, 32], and (iv) morphological [99], and (v) circuit motifs [74, 96]. Think about starting with a literature search if you pursue any of these alternatives.

Challenges: The math can be somewhat daunting if you don't have the necessary background in algebraic topology. However, the tools are simple to use and the results relatively easy to interpret. Look at Pawel Dlotko's calendar entry from last year for an introduction to simplicial complexes and persistent homology. You might also look at the Python package called NeuroBot that I wrote using his simplicial-complex library—called NeuroTop—to analyze the seven-column dataset.

April 13, 2017

Notes from Adam Marblestone's presentation on April 13 [...] motivated by Greg Wayne's observations concerning our [105] paper in Science [...] the role of loss functions in shaping artificial and natural neural-network representations [...] interesting to think about how sparse coding plus natural image reconstruction autoencoders fit into the overall picture [...] L1 —least absolute deviations (LAB) and L2 —least squared error (LAE)—norms used as loss functions versus regularization term [...] both representation and coding as inherently distributed and time varying (think of indefinitely prolonged development) [...]

[...] learning by twiddling coefficients using differences to guide search, i.e., node perturbation [...] the Francis Crick quote damming back propagation as a biologically implausible learning mechanism [...] weight transport [...] solved by having completely bidirectional weight matrices [...] result using random matrices (HTML) [...] Blake Richards [...] combined with random feedback weights solves the problem of weight transport and explains the morphology of pyramidal neurons [...] Walter Senn [...] Geoff Hinton and Yoshua Bengio [...] context encoders aren't supervised [...] what can't you do with back-prop and reconstruction loss [...]

[...] Issa, Cadieu and DiCarlo [80] (HTML) provide evidence that the ventral stream computes errors [...] computes a perceptual signal, takes feedback to compute a local loss reflecting its "change of mind" [...] Elias Issa et al synthesis / synthetic gradient propagation [...] Shimon Ullman's internally-generated bootstrap cost functions [...] faces are often looking at hands [...] embedding spaces, skipgram models and Adam's learning-from-context example in image understanding [...] prediction as a general cost function [...] acetylcholine in cortex (glial pathway) versus dopamine in the basal ganglia [...] hippocampus as a three layer cortex but optimized for very specialized computations [...]

[...] attractors in thalamocortical recurrent loops [...] difference between short (quasi-stable encodings, depending on sustained reentrant patterns of activation) and longer term (consolidated encodings) in terms of the mechanisms involved in initiating memory formation, maintaining the necessary state information in a quasi-stable form and then consolidating the nascent engram into a more-or-less stable (at least long-term and perhaps more energy efficient) representation that is superficially reminiscent of the difference between dynamic (needing periodic refresh) and static (not needing static refresh) RAM.

P.S. In email to me, Konrad Kording and Greg Wayne, Adam wondered if this paper [55] might explain where cost functions for the different cortical areas live:

Basal forebrain cholinergic neurons influence cortical state, plasticity, learning, and attention. They collectively innervate the entire cerebral cortex, differentially controlling acetylcholine efflux across different cortical areas and timescales. Such control might be achieved by differential inputs driving separable cholinergic outputs, although no input-output relationship on a brain-wide level has ever been demonstrated. Here, we identify input neurons to cholinergic cells projecting to specific cortical regions by infecting cholinergic axon terminals with a monosynaptically restricted viral tracer. This approach revealed several circuit motifs, such as central amygdala neurons synapsing onto basolateral amygdala-projecting cholinergic neurons or strong somatosensory cortical input to motor cortex-projecting cholinergic neurons. The presence of input cells in the parasympathetic midbrain nuclei contacting frontally projecting cholinergic neurons suggest that the network regulating the inner eye muscles are additionally regulating cortical state via acetylcholine efflux. This dataset enables future circuit-level experiments to identify drivers of known cortical cholinergic functions. [SOURCE]

April 11, 2017

This class is all about scaling computational neuroscience to work with large datasets. Here are some of the datasets that you may use for course projects. As with all of the data made available for projects relating to this class, the data was shared with the understanding that it is to used for your sole use in this class, it cannot be shared with anyone outside the class, and, if you have aspirations to publish a paper or present a poster referring to any use of this data you must first obtain the consent of the owner, who is generally the director of the lab that produced the data in the first place. Here is an introduction to the datasets:

April 9, 2017

Here are examples of computational advances resulting from the study of relatively simple organisms, including the common fruit fly (Drosophila melanogaster, house mouse (Mus musculus) and larval zebrafish (Danio rerio) that have or likely will have an impact in developing algorithms that further the state of the art in artificial intelligence:

Unlike more general insights that have their origins in the cognitive and behavioral neurosciences, e.g., reinforcement learning, Hebbian learning, associative memory, the examples above provide specific algorithmic insights of a sort we have barely begun to mine from our study of functional connectomics. I expect the microscale architecture of the brains of diverse organisms and their functional analysis will yield a windfall of engineering insights that will be translated into hardware and software for solving very different problems than those originally solved by natural selection.

Moreover the sort of architectures we are proposing for inferring such knowledge from data are themselves relevant to artificial intelligence insofar as these architectures enable us to infer models of complex dynamical systems, including new classes of artificial neural networks that extend the possibilities of current DNN's and DQN's that either optimize or synthesize new neural network architectures [188, 94]. By the way, Geoff Hinton had a huge influence on the development of predictive coding and hierarchical and Bayesian extensions.

I emphasize Drosophila in large part due to our collaboration with Janelia and the fact that Neuromancer working with HHMI is very likely to have the complete connectome by the end of this year if not sooner. The Zebrafish is attractive for different but similarly compelling reasons. It is a vertebrate, with a close homolog of the basal ganglia which is central to our understanding of reinforcement-based learning. DeepMind and Google Brain are substantially invested in temporal difference reinforcement learning, how intrinsic reinforcement signals are incorporated into the framework, how to make it more efficient, and so forth. DeepMind explicitly mentions the striatal inspiration in their work—see the above-linked review in Current Biology and the paper that it refers to [165] for background on the relationship between the striatum and basal ganglia.

The Zebrafish is the simplest, most accessible system in which we can comprehensively measure and model reinforcement learning in a close analog of the mammalian striatum and basal ganglia. It can learn complex sensorimotor tasks by reinforcement, using systems analogous to mammals, and yet is a preparation in which this entire process can be comprehensively studied. The overall expediency of the system is key: The functional imaging is simply better than in anything else, even C. elegans, and it is of a sufficiently small size where we can readily imagine getting a complete connectome for a functionally imaged organism—indeed I'm already talking with two teams, Seung's lab at Princeton and Lichtman's at Harvard to do just that. If we want to understand how reinforcement learning actually works in biology, this system is perfect.

Caveats: As far as I can tell, we don't truly have good models either of the dopamine signals themselves or of how they shape the basal ganglia's action selection policy. Or mechanistically of how action selection works. As far as I know, there are a few BG action selection models like the direct / indirect pathway model [64, 65] and work by Gurney, Prescott and Redgrave [173, 66], but little is really known about how exactly this works in reality. Recent papers showed spatial clustering of striatal medium spiny neuron responses, for example—what is the significance of this? How does the BG manage the huge convergence of inputs from all around the brain and reduce it into a small set of output dis-inhibitory actions. Then, exactly what influence does this output have on the thalamus [114]—also see here and here. A similar state of affairs probably holds for basal forebrain cholinergic systems, which at least in mammals have a reinforcement signaling role. [Thanks to Adam Marblestone for his contributions to the above. The example pertaining to the basal ganglia is largely due to Adam.]

April 7, 2017

Excerpts from Daniel Dennett's Bacteria to Bach and Back: The Evolution of Minds [35] prompted by a discussion with Robert Burton:

Words are the lifeblood of cultural evolution. (Or should we say that language is the backbone of cultural evolution or that words are the DNA of cultural evolution? These biological metaphors, and others, are hard to resist, and as long as we recognize that they must be carefully stripped of spurious implications, they have valuable roles to play.) Words certainly play a central and inelliminable role in our explosive cultural evolution, and inquiring into the evolution of words will serve as a feasible entry into daunting questions about cultural evolution and its role in shaping our minds. […]

In both cases — it is possible that life, and language, arose several times or even many times, but if so, those extra beginnings have been extinguished without leaving any traces we can detect. […] Dawkins (2004, pp. 39-55) points out that, in many languages, tree diagrams showing the lineages of individual genes are more reliably and formatively traced than the traditional tree showing the dissent of species, because of "horizontal gene transfer"—instances in which genes jump from one species or lineage to another. […]

Sometimes, failure to find the word we are groping for hangs us up, prevents us from thinking through to the solution of a problem, but other times we can wordlessly make do with unclothed meanings, ideas that don't have to be in English or French or any other language. [Jackendoff 2002, especially chapter 7, "implications for processing," is a valuable introduction.] Might wordless thought be like barefoot waterskiing, dependent on gear you can kick off once you get going? […] An interesting question: could we do this even if we didn't have the neural systems, the "mental discipline," trained up in the course of learning our mother tongue? […]

The idea that languages evolve, that words today are the descendants in some fashion of words in the past, is actually older than Darwin's theory of evolution of species. Text of Homer's Iliad and the Odyssey for example were known to descend by copying from text descended from text descended from text going back to their oral ancestors in the Homeric times.

Commentary:

The evolution of language and especially the language of scientific disciplines, is subject to more rigorous, less forgiving interpretation / selection pressure, for example, by "correcting" contextually inappropriate inferences drawn from analogies that have otherwise proved to be useful in understanding complex phenomena. Induced mutation in the form of variable substitution and the inclination to "fill in" a missing term in an analogy is an exercise that can yield new insights and extensions to a theory, but can also demonstrate the limitations of a given concept or analogy, by inviting increased scrutiny that ultimately undermines the value of an analogical framing of a concept or theory altogether. It remains to see whether the DNA analogy illuminates or distorts our understanding of language and linguistic variation.

For some reason, the concept that came immediately to mind when I read this excerpt had to do with a meme introduced into computer science and its relevance to document search, namely "the long tail" of a distribution where lie the obscure queries and their preferred less commonly known content of all stripes that distinguishes a search engine like Google from those with less coverage that fail on queries in the long tail. As an undergraduate math major, I was fascinated with long tails in a careless way, not really distinguishing between density plots where the area under the curve is equal to 1, and plots of arbitrary positive-valued functions where the area under the curve might not even be bounded.

Sequences that converge to zero but that the residues — the sum of terms to the right of any given term — are always infinite, e.g., the harmonic series: 1 + 1/2 + 1/3 + 1/4 + … were especially interesting. Learning about them provided my introduction to the "plug and replay" approach to doing science10. Given the concept of a "series whose terms converge to zero but whose residues sum to finite numbers" leads inexorably to the question of what happens when you substitute "sum" with "do not sum". So much of mathematics and physics arise out of making such substitutions and working through the consequences. Of course, you’d need the notion of infinite sums and, eventually, the notion of transfinite numbers, but, as Cantor discovered, that sort of thinking can lead to madness.

April 5, 2017

Here is the somewhat long-winded note I sent to selected contacts in several of our collaborating academic and privately-funded research institutes asking them for examples of research on functional connectomics potentially leading to results of interest to Google. The length can be explained in part due to my remarks reassuring them that such a project would be open in terms of sharing the data and tools we generate in our collaborations with external labs:

If Google builds a team to conduct research on functional connectomics, it will do so for two reasons, (a) the particular focus of the research demands the scale of computational resources that only Google and a handful of other corporations can possibly muster, and (b) that Google believes the anticipated products of this research will be beneficial to the scientific enterprise and potentially to human health and welfare.

If it does build such a team, then it is likely that a good portion of the effort would be directed at building tools useful to the scientific community and that these tools would be made available without cost. Moreover Google would very likely partner with a number of academic labs and privately funded research institutes, such as the Allen Institute for Brain Science, the Howard Hughes Medical Institute, and the Max Planck Institute, to name a few with which we have had fruitful collaborations in the last few years.

If past is prologue, then Google will advocate that the fruits of these collaborations, in terms of research products such as high-volume recordings of neural activity and their analyses, will also be made available to the scientific community, and we will negotiate the precise conditions under which such data will become available, working with our partners to accommodate their self interests in terms of academic priority in publishing.

The above three paragraphs are intended to make clear both the conditions under which Google would proceed in developing such an effort, and its expectations in terms of collaborating with diverse teams expert in the underlying neurobiology. It would not likely replicate the expertise within the community, and the existence of such expertise and willingness of those possessing such expertise is a precondition for our embarking on an effort to accelerate this area of science.

For efforts that require a substantial outlay of capital to provide the necessary computing resources and pay the engineers that would develop the underlying technology, Google would very likely add an additional condition that the knowledge gained would provide some benefit to Google in terms of new technologies that might ultimately find their way into products. This has been the case for project Neuromancer and will likely be the case for any reasonably well staffed project that requires more than a few quarters to complete.

Having set the stage, I'll now outline what I need from you to help me make the case for starting a project in functional connectomics, complementing our existing project focusing on structural connectomics:

A list of noteworthy fundamental scientific results that such a project might reasonably generate in collaboration with its partners. It would be more compelling if that list also includes a description of the enabling technologies required to achieve said results and an estimate of the time required to develop said technology.

In the case of studying the brain, it is natural for Google to be interested in the prospects for the knowledge gleaned from such studies to further the development of technologies that are important in improving our products and services, and in particular those that pertain to image understanding, robotics, natural language understanding, artificial intelligence and large-scale computing and networking.

If the anticipated fruits of the scientific effort enabled and accelerated by Google’s involvement are unlikely to lead to the development of such useful technologies, that outcome would likely undermine Google's interest in making such an investment. This does not reflect Google's disinterest in the scientific enterprise, but rather the line between Google's responsibilities to its investors and the economic well-being of the company, and its aspirations vis-à-vis corporate philanthropy and on-going efforts to contribute to the health and welfare of its employees, customers and society in general.

April 3, 2017

What is a scientific theory and what use is it?

Consider, Ptolemy's "geocentric theory" with the earth as the center of the universe and his "epicycles" that were required to make the theory fit the data, Aristotle's "geocentric celestial spheres" sustained the geocentric conceit until the 17th century, Copernicus and his much maligned "heliocentric theory" with the sun as the center of universe, and Galileo who was tried and found guilty of heresy for his belief that the "sun" was the center, thereby disagreeing with the church's self-serving interpretation of the bible which already had multiple layers of interpretation. Galileo was an instrument builder, data driven experimentalist and, for his time, mathematically sophisticated theorist; he substantially improved the best telescopes of the time by grinding his own lenses and carefully tracked the position of the planets in the night sky to support his theory. Newton changed the way astronomers did science. He invented the first practical reflecting telescope, replacing the refractory telescope with the reflector telescope for all but the smallest instruments, he was incredibly careful in making his observations, and was, for all intents and purposes, the first [human] computer to solve differential equations in order to fit the data, concluding that the planets followed elliptical orbits around the sun. It is difficult for us to comprehend the degree to which he accelerated the advance of science and influenced the way we conduct science today.

Not all self-proclaimed scientists pursue their scientific interest as methodically as Newton. In some disciplines, data is hard to come by, in others it is difficult to conceive of how to build mathematical models of the sort Newton championed, and, in still others, what is accepted as a theory is more like a parable or fictionalized account of the observed phenomena. Not all phenomena yield to the methodology of science as Maxwell, Rutherford, Einstein, Crick and Watson, Hodgkin and Huxley etc would recognize it. What is a "good" model or theory? To begin with it should be "usefully" explanatory and predictive, not a "just so" story: "The Leopard used to live on the sandy-colored High Veldt. He too was sandy-colored, and so was hard for prey animals like Giraffe and Zebra to see when he lay in wait for them. The Ethiopian lived there too and was similarly colored. He, with his bow and arrows, used to hunt with the Leopard. [...] Then the prey animals left the High Veldt to live in a forest and grew blotches, stripes and other forms of camouflage." [...] "So the Ethiopian changed his skin to black, and marked the Leopard’s coat with his bunched black fingertips. Then they too could hide. They lived happily ever after, and will never change their coloring again." — How the Leopard got His Spots by Rudyard Kipling. Scientists working in evolutionary biology are often accused of generating "just so" stories, but many theories start out that way.

How do the best theories stand up to scrutiny?

A. Newtonian celestial mechanics: [POSITIVES] accurate prediction of planetary motion, mathematically elegant — Dirac's "the unreasonable effectiveness of mathematics", broad application — no need for a separate theory of terrestrial motion, or a separate method for estimating the orbits of asteroids, comets or any other macroscale objects; no prime mover — apparently this didn't upset Newton's religious views as he simply pushed the problem back another step and had God [of the old testament variety] create gravity; [NEGATIVES] invokes spooky action at a distance, doesn't accord with the general theory of relativity (Einstein), doesn't predict space-time curvature (Minkowski) and how massive bodies can deflect even light, and doesn't account for quantum effects — but then neither does Einstein's theory.

Ptolemy and Aristotle gave us the "geocentric theory", "celestial spheres" and "the unchanging celestial realm". The Catholic church took their word as God's; Why? Copernicus was derided for his "heliocentric theory", but luckily he as ignored by the Vatican. Tycho Brahe discovered "super novae", demonstrated that stars come and go and discredited the "unchanging celestial realm" theory. Kepler offered his "three laws of planetary motion". Galileo improved the refractor telescope, showed us how to collect good data and perform experiments to test hypotheses and then ran afoul of the Inquisition, barely escaping with a life in exile. Newton built one of first reflector telescopes in an instance of parallel invention and then vastly improved its design winning him "early admission" into Royal Society, then, as an afterthought, invented the calculus, predicted the elliptical orbits of planets, and spent a few years breathing toxic fumes while playing at alchemy.

Some of these theories seem ludicrous to us today but all of them are false, some more than others, some egregiously so. In fact according so a study "Most published research findings are false" Annual Review Statistics and its Applications. 2017, according to a 2015 paper appearing in Science "Fewer than half of 100 studies published in 2008 in three top psychology journals could be replicated successfully, and then in 2015 we read "Biomedical Science Studies Are Shockingly Hard to Reproduce". Who here popped vitamin C like candy in the 60's, stopped consuming fat in the 80's or eliminated carbohydrates entirely from their diet and ate only red meat in the oughts.

"The best [summary description of natural selection], for simplicity, generality, and clarity is probably [that of] philosopher of biology Peter Godfrey-Smith: Evolution by natural selection is change in a population due to (i) variation in the characteristics of members of the population, (ii) which causes different rates of reproduction, and (iii) which is heritable. Whenever all three factors are present, evolution by natural selection is the inevitable result, whether the population is organisms, viruses, computer programs, words, or some other variety of things that generate copies of themselves one way or another. We can put it anachronistically by saying that Darwin discovered the fundamental algorithm of evolution by natural selection, an abstract structure that can be implemented or "realized" in different materials or media." — From Bacteria to Bach and Back: The Evolution of Minds by Daniel Dennett.

B. Darwinian natural selection: in a nutshell, if there is a source of variation in the traits of organisms, and these traits differentially impact reproduction, and there is a mechanism whereby organisms can pass on traits to their offspring, then natural selection will prefer species that have more offspring: no explanation of a mechanism for how traits are passed on from one generation to the next — this will have to wait for the rediscovery of Mendel's work by Bateson and others and the work of Crick and Watson and their colleagues in determining the molecular structure of DNA and the role of genes in building bodies; no explanation of how variation arises naturally and how it can alter reproductive success — this will have to wait for the discovery of mutations and early demonstrations that even point mutations can have a devastating impact on the ability of an organism to pass on traits and introduce new traits that confer a selection advantage or disadvantage; to his credit Darwin did understand that the process of natural selection could take a long time to to produce new species.

As an example of a theory run amok, "Ontogeny recapitulates phylogeny" is a catchy phrase coined by Ernst Haeckel, a 19th century German biologist and philosopher to mean that the development of an organism (ontogeny) expresses all the intermediate forms of its ancestors throughout evolution (phylogeny). Haeckel's theory was large discredited but surfaces from time to time just like the face of Jesus turns up regularly on tortillas, cloud formations and slices of burnt toast.

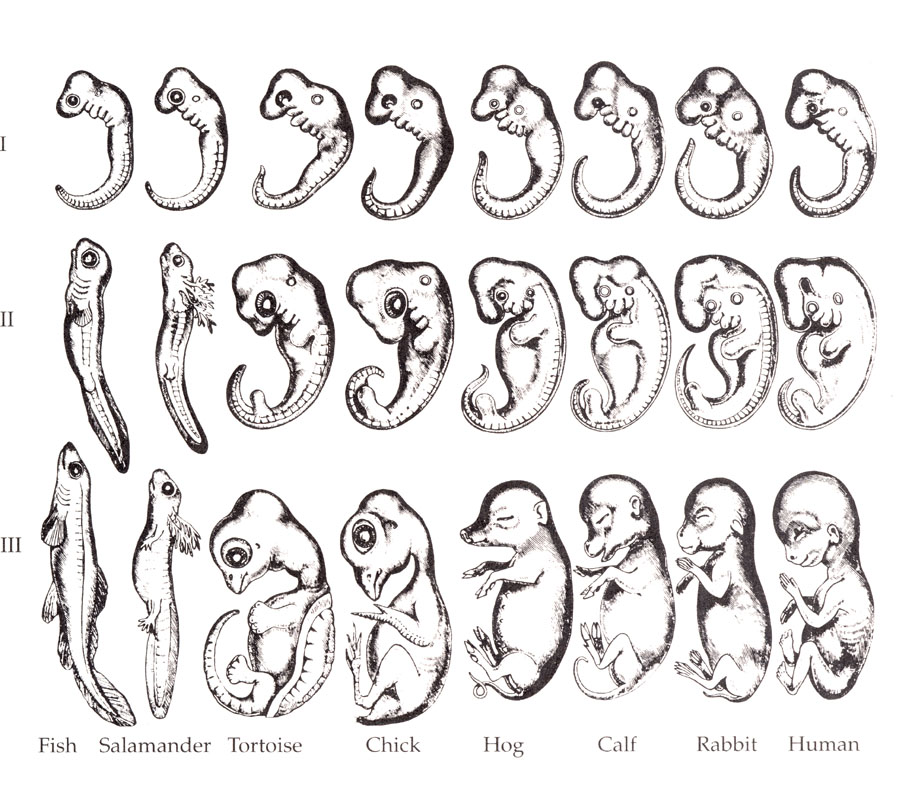Referred to as the Theory of Recapitulation, it was meant to be a synthesis or reconciliation of Lamarckism and Darwinism. It has a long history going back to the Pharaohs and was originally used to explain how children's use of language gives insights on its origin and evolution. For the most part, the theory has been discredited in biology but still lingers on in some linguistic theories. Is the theory wrong? How would we know? It sounds plausible? Maybe it applies to language but not biology? Why does it appeal to us in the first place?

We won't be fooled again! — The Who

If you believe astrophysicists who write books or produce documentaries like Sean Carroll and Neal deGrasse Tyson, then you probably believe that [physicists] know all the fundamental particles and associated forces that can interact with the human body or influence human destiny in any way ... that's ANY way and not just any DISCERNIBLE way. There are particles and forces that we don't understand and possibly some that we don't know even about, e.g., beyond gravitons and Higgs bosons, but they don't interact with us, nor do they operate on spatial or temporal scales that could make a difference in our lives or those of our offspring. — Carroll says that if paranormal powers were possible scientists would have detected them, and suggests quite reasonably that if God [of the old testament variety] exists we would have detected him and since God doesn't register on any of our sensitive instruments then he can't have any impact on our lives. I think Carroll is right — Cartesian dualism is dead, but he is quick to point out that his claims are merely hypotheses albeit hypotheses that are almost overwhelmingly supported by the data. We could be wrong. We could be fooled again. It's just not very likely.

Just prior to the beginning of the 20th century, "There is nothing new to be discovered in physics now. All that remains is more and more precise measurement." — this quote which is often misattributed to William Thomson, Lord Kelvin, is more likely a paraphrase of Albert A. Michelson — of Michelson-Morley fame — who in 1894 stated: "[...] it seems probable that most of the grand underlying principles have been firmly established [...] An eminent physicist remarked that the future truths of physical science are to be looked for in the sixth place of decimals." An interesting combination of hubris and pandering to authority. It used to be that it wasn't true unless Socrates said so, and, conveniently, we don't know what Socrates said because he never wrote anything down. He left the scribbling to his protege Plato who apparently took it upon himself to write down everything that Socrates did say or might have said. A sure recipe for some creative writing.

My friend Mario Galarreta [50, 49, 48, 46, 47] is fond of saying [or showing with a Venn Diagram] that if all that WE KNOW is in a small box A, then the box B containing A and all the things WE KNOW THAT WE DON'T KNOW is substantially larger, and the box containing A, B and all the things WE DON'T KNOW THAT WE DON'T KNOW is much larger than either A or B. Perhaps some of you remember Donald Rumsfeld. "Reports that say that something hasn't happened are always interesting to me, because as we know, there are known knowns; there are things we know we know. We also know there are known unknowns; that is to say we know there are some things we do not know. But there are also unknown unknowns — the ones we don't know we don't know. And if one looks throughout the history of our country and other free countries, it is the latter category that tend to be the difficult ones." — Secretary of Defense, Donald Rumsfeld answering a question during a Department of Defense news briefing in 2002. Rumsfeld attributed the key phrase, "unknown unknowns" to William Graham, the Director of the White House Office of Science and Technology Policy during Ronald Reagan's administration.

In August of 2015, the Smithsonian ran an article reporting: "According to work presented today in Science, fewer than half of 100 studies published in 2008 in three top psychology journals could be replicated successfully. The international effort included 270 scientists who re-ran other people's studies as part of The Reproducibility Project: Psychology, led by Brian Nosek of the University of Virginia." A similar study published the same year ran with the title "Biomedical Science Studies Are Shockingly Hard to Reproduce", and one idiot — more charitably, "one well-meaning, technically-correct, but politically-naive and dangerously-incendiary loose cannon" — wrote, referring to the article in Science, "This project is not evidence that anything is broken. Rather, it's an example of science doing what science does. [...] It's impossible to be wrong in a final sense in science. You have to be temporarily wrong, perhaps many times, before you are ever right." Donald Trump would so agree. Why do scientists publish work that can't be reproduced, manipulate data to their advantage and fudge the statistics to make their case? Perhaps they are not maliciously trying to fool their colleagues. Perhaps we are constitutionally challenged when it comes to reporting our findings.

"The observer-expectancy effect (also called the experimenter-expectancy effect, expectancy bias, observer effect, or experimenter effect) is a form of reactivity in which a researcher's cognitive bias causes them to subconsciously influence the participants of an experiment. Confirmation bias can lead to the experimenter interpreting results incorrectly because of the tendency to look for information that conforms to their hypothesis, and overlook information that argues against it. It is a significant threat to a study's internal validity, and is therefore typically controlled using a double-blind experimental design." — https://en.wikipedia.org/wiki/Observer-expectancy_effect This is just one of many cognitive biases that cloud human decision making. Much of the original research such as the behavioral economics of Daniel Kahneman and Amos Taversky initially met with a great deal of skepticism, but now there a veritable cottage industry of psychologists and behavioral scientists coming up with new biases and aberrant behavior — possibly itself flawed by the very biases they seek to uncover:

Will the real theory please stand up?

Our understanding of gasses is perhaps best articulated in a series of theories — quantum mechanics (QED) → the kinetic theory of gasses → fluid dynamics — that operate at different spatial and temporal scales and invoke different assumptions, physical laws, language and mathematics. The notion of "emergence" is often maligned by scientists as a politically-correct alternative to admitting ignorance. In some disciplines and some theoretical accounts, however, emergence is a natural consequence of simplifying our understanding of complex phenomena to make them more tractable mathematically and computationally in order to facilitate analysis or prediction.

"Seeing how relatively easy it is to derive fluid mechanics from molecules, one can get the idea that deriving one theory from another is what emergence is all about. It’s not — emergence is about different theories speaking different languages, but offering compatible descriptions of the same underlying phenomena in their respective domains of applicability. If a macroscopic theory has a domain of applicability that is a subset of the domain of applicability of some microscopic theory, and both theories are consistent, then the microscopic theory can be said to entail the macroscopic one; but that’s often something we take for granted, not something that can explicitly be demonstrated. The ability to actually go through the steps to derive one theory from another is great when it happens, but not at all crucial to the idea." — from The Big Picture: On the Origins of Life, Meaning, and the Universe Itself by Sean Carroll.

There are many more neurons conveying information "down" the visual stream from higher association areas back toward the primary (striate) cortex than there are neurons conveying information "up" the visual pathways initiating in the retina, traveling along the optic tract, crossing over to the opposite hemisphere, moving through the mysterious pathways—it probably isn't "just" a relay station"—of the lateral geniculate, being processed (to some degree) in the striate cortex prior to splitting out into multiple (sub) streams and feeding into a dozen or more (additional) retinotopic maps before "combining" in the inferotemporal cortex and upstream association areas. Why? From Hubel and Wiesel [77, 76, 75] onward part of the answer has been "hierarchy" — if you haven't seen it, check out the "One Word: Plastics" scene in "The Graduate" starring Dustin Hoffman. But now we're more sophisticated, now the word is a phrase "Bayesian hierarchical predictive coding" and neuroscientists are scrambling to determine if it's "right" or "wrong" [70, 156, 44] (these papers are a very small sample of what is now a veritable cottage industry if academics churning our papers on predictive coding ... not all at once, fads come and go and then come again.

On the white board, draw simple control-theory view of systems neuroscience: → controller → physical plant → feedback. Now play around with labeling the components: the Atari game console, the physics engine, the game controller, the CRT or LCD screen, a person playing the game, etc. Now imagine ... a fly with a tiny bundle of wires protruding from its brain and leading to a two-photon (fluorescent) excitation (2PE) microscope ... or implanted with one of the miniature fluorescent microscopes developed in Mark Schnitzer's lab [84, 57, 13, 54]. Now go wild and imagine a fruit fly walking on a tiny ball tethered to a microscale fiber optic capable of limited flight ... Read the controversial, thought-provoking paper by Eric Jonas and Konrad Kording [86] entitled Could a neuroscientist understand a microprocessor?.

March 31, 2017

Email exchange with Grace Hunyh in Ed Boyden's Lab regarding my presentation at MIT last week:

GHH: First, have you tried your framework on smaller systems, e.g., like the crab stomatogastric ganglion (STG) which has only 30 neurons? There is less data available since fewer researchers study it, but it is interesting because it can be completely dissected from the crab and the neurons are large and easy to probe electrically.

TLD: Too small a circuit, not varied enough in function or network complexity to support learning. The only way I can get sufficient scale in the near term is to either record from hundreds or thousands organisms of the same genotype or a single phenotype with thousands or millions of different isolatable sub circuits / candidate motifs.

GHH: Second, assuming your framework learned a mesoscale model, would the model represent an "idealized" organism or how would we correlate the model with the individual variability we know exists between animals?

TLD: Take a close look / listen at the transcript and video I sent out earlier this morning, If everything works like I'm expecting it will, the parts of the model that correspond to the functional module basis functions will represent the genotype whereas the module interfaces will capture the variability among genotypes.

GHH: Third, assuming the framework was working, what do you think are the lowest hanging fruit in terms of behavior that you think your system can explain/predict? Do you think the framework would be able to suggest novel and actionable interventions in living systems and how would we "close the loop" between the model and experiment

TLD: First, I want to see if the functional basis captures the sort of homogeneity of function one might expect in mouse visual cortex, and fly lamina, medulla and lobula. I'd also like to see if the model can identify common functional motifs in such diverse regions as the central complex, olfactory system and mushroom bodies.

I'd like to see if the complexity of functional motifs in evolutionarily more recent sub circuits such as mammal neocortex is less than that found in older systems such basal ganglia and the cerebellar cortex, and, if we find inherent functional variability in cortex as some suggest, how primary sensory areas differ from, say, prefrontal regions involved in executive control and planning.

Note that none of these use cases require that the functional module networks are transparently explanatory; they just have to capture conserved, broadly replicated function and in so doing reliably serve as markers for functional motifs.

April 2, 2017

Email exchange with Daniel Dennett concerning Chapter 8 in his most recent book: I don't know about the Deacon work, but I think there are forces at work that will ultimately select for many of the features we are enamored of in biological systems. While obviously on a much larger scale than any organic computing technology, data centers are by necessity becoming self-healing, self-correcting, and automatic-load-balancing using AI technology, working with the—not particularly intelligent—national electric grid to shift work to off-peak times and micromanage standard maintenance like running diagnostics, checking disk drives for errors, and a myriad of other janitorial work that has to be done to keep a data center running at peak efficiency.

For some years now, cyber-security engineers have employed the metaphor of building an immune system to notice denial-of-service attacks, worms, and other malware and taking immediate steps to mitigate the damage and reroute traffic to other data centers if the damage threatens critical infrastructure or software systems responsible for managing user data or is predicted to result in a significant increase in latency. If past is prologue, then these technologies will increasingly rely on machine learning techniques, become simpler, faster, impregnable, and over time insinuate themselves ever deeper into the hardware and software so that at some point they will be simplified to the point where they can be physically integrated right down to the chip level and beyond.

When I say beyond the chip level, I mean the hardware analog of the cellular level, corresponding to individual components embedded in the silicon and connected by traces a few nanometers in width etched into the silicon. Already engineers at IBM, Intel, AMD, Nvidia and Hewlett-Packard are trying to tame the behavior of transistors operating in the subthreshold regime, promising ultra-low-power measured in pico watts, but reliability is constantly threatened by micro thermal changes and fluctuating capacitive current leakage.

Building circuits constructed of components operating in the subthreshold regime is incredibly difficult as Carver Mead warned his graduate students and colleagues interested in building neuromorphic computing devices. Mead essentially counseled, if you’re going to build ultra-low-power devices using semiconductors and subthreshold voltages, then your best bet is to learn from biological computing, assume that your primitive components are flaky, unpredictable computing units, and make your devices reliable by combining several flaky primitive computing units to make each reliable unit.

At the rate of sophistication and miniaturization we are seeing in nanotechnology, we may be able to to go one better by adding nanoscale feedback loops to enable primitive computing units that operate together to agree on the meaning of voltage levels as they pertain to intended interpretations, for example, propagating binary information or using some form of rate coding. A combination of a signal-boosting repeater and impedance matching circuit that operates on a pair-wise basis on each trace connecting two components analogous to the constant flux that goes on between the pre-synaptic neuron's axon terminal and the post-synaptic neuron's dendritic spine. Memristive phase-change devices such as those that make PRAM technology possible offer interesting options in this design space.

One last comment, if I was betting, I would pour more money into building better AI’s by exploiting the rapidly increasing capabilities of existing AI's and building completely automated fabrication facilities so the AI’s could do the rapid prototyping for developing new self-healing, local-signal-matching technology themselves in much the same way as pharmaceutical companies are now using AI technology to design (in silico) and test (in vivo) using induced pluripotent stem technology to grow designer organelles in a petri dish to run hundreds or thousands of experiments at once in highly parallel assembly lines.

It would be really interesting to build such an AI. Among other challenges you’d have to work to avoid introducing human biases. I expect you’ve seen how tentative adults behave who have not been exposed to technology until their twenties, it’s as if the laptop or cellphone is going to explode or be damaged permanently by just hitting the wrong button. Children on the other had are fearless, and they poke, shake, and smear food on a new device with wild abandon and mischievous glee. An AI with the ability to dream up and filter thousands or millions of experiments, and then run hundreds or thousands of those experiments in meat time should have the same fearless zeal.

March 2, 2017

In attempting to simplify the terminology I use in giving talks about mesoscale modeling and tailor the delivery to different audiences as well as mixed audiences, I looked in the literature for consensus about the meaning of the terms used by computational neuroscientists and computer scientists working on computer-vision and image-processing problems to talk about convolutions. Here are the best sources I found for the use of the terms receptive field and filter kernel:

When dealing with high-dimensional inputs such as images, as we saw above it is impractical to connect neurons to all neurons in the previous volume. Instead, we will connect each neuron to only a local region of the input volume. The spatial extent of this connectivity is a hyperparameter called the receptive field of the neuron (equivalently this is the filter size). (SOURCE)

In addition to the definition below, the term filter kernel is often used as a synonym for kernel function when speaking about the obvious generalization of convolution. Different disciplines talk about filters as predicates on structured lists, tables or tensors. The term is also used in machine learning, especially with regard to support vector machines that are also referred to as kernel machines. In many but not all cases, the kernel function is the dot product of the convolution matrix and a filter-sized region of the target data, i.e., matrix, volume or other structured data.

In image processing, a kernel, convolution matrix, or mask is a small matrix. It is useful for blurring, sharpening, embossing, edge detection, and more. This is accomplished by means of convolution between a kernel and an image. (SOURCE)

In functional programming, a filter is a higher-order function that processes a data structure (usually a list) in some order to produce a new data structure containing exactly those elements of the original data structure for which a given predicate returns the Boolean value true. (SOURCE)

February 26, 2017

The paper has gone through several iterations aided by feedback from David Cox and Olaf Sporns and students and faculty who attended my presentations at the Berkeley Redwood Institute and Lawrence Berkeley National Labs. Based on their feedback I worked on the figures and generated a new set of slides that I'll present at the Keystone Symposium on Molecular and Cell Biology next week in Santa Fe. The slides are available here.

For each of the slides with graphics, I linked the slide title to the corresponding figure in the current draft of the paper. That should make it pretty easy to get the basic idea, and by following the links you can drill down as deep as you like modulathe uneven quality of the draft. The paper is in disarray since the rest of the text hasn't caught up with the figures. After the Santa Fe trip, I'm back in MTV for a week before heading out again to making a speaking tour of the East coast. I'll be giving talks at HHMI Janelia in Washington DC, Princeton in NJ, Columbia in NYC, and finally Harvard and MIT in Cambridge.

December 7, 2016

The first draft of the Mesoscale Computational Modeling paper is available here.

Automatically Inferring Mesoscale Models of Neural Computation

 Abstract 

We examine the idea of an intermediate or mesoscale computational theory that connects a molecular (microscale) account of neural function to a behavioral (macroscale) account of animal cognition and environmental complexity. Just as digital accounts of computation in conventional computers abstract from the non-essential dynamics of the analog circuits implementing gates and registers, so too a computational account of animal cognition can afford to abstract from the non-essential dynamics of neurons. We argue that the geometry of neural circuits is essential in explaining the computational limitations and technological innovations inherent in biological information processing. We describe how to employ tools from machine learning to automatically infer a satisfying mesoscale account of neural computation that combines functional and structural data in the form of neural recordings and morphological analyses with physiological and environmental data in terms of behavioral recordings. Rather than suggest a specific theory, we present a new class of scientific instruments that enables neuroscientists to propose and test mesoscale theories of neural computation.

1  Introduction to Mesoscale Models

1.1  Mesoscale Models of Biological Computation

A mesoscale computational model is constructed from components corresponding to algorithmic representations that explain the activity of ensembles of simpler components at the micro / molecular scale, and that can be combined in different configurations to generate activity at a macro / behavioral scale. For example, algorithms described in assembly language can explain aggregate activity at the level of bits and processor opcodes, while also providing a language in which to describe how the subroutines used to manipulate a spreadsheet or edit a document give rise to the behavior we observe on a computer screen. A mesoscale model bridges the gap between the micro and the macro scales. The mesoscale components are essentially mathematical abstractions that play the role of hidden variables in a statistical or machine-learning model.

Mesoscale models generally achieve their explanatory power in part by ignoring some details regarding activity at the microscale. Hence, there is not a one-to-one correspondence between events at the microscale and those at the level of description provided at the mesoscale11. Ideally, such a model is both predictive and diagnostic12, but its defining characteristic is that it provides a computational account of aggregate activity at the microscale, ignoring some microscale detail, while convincingly and comprehensively explaining those aspects pertaining to computation that directly contribute to behavior at the macro scale. This definition is reasonably complete with one glaring exception: What exactly is computation?

The sort of mesoscale model discussed here is called an emergent theory by physicists. The term is often colloquially misused, hence the qualification to its application in physics. One can formulate a coherent theory of gasses in terms of quantum electrodynamics, kinetic particle theory, or fluid dynamics. The fluid account emerges out of the kinetic account which emerges out of the quantum account. All three theories are correct given an appropriate context for their application, though they vary considerably in terms of the range of phenomena they can practically—versus theoretically—explain. An emergent theory is derivable from the theory it emerges from. The converse is not true.

Emergent theories make assumptions to simplify understanding and facilitate computation. In the case of the mesoscale model discussed here, the primary simplifying assumption is that microscale circuits employ ensembles13 of neurons because individual neurons are not particularly reliable computing devices. They have to work together to achieve a composite level of reliability sufficient to ensure the survival of the organism. Of course, some neural computers are more reliable than others. Implementing biological computing with neurons is a little like implementing computing elements using semiconductors operating in the subthreshold regime: you do it to save power, but it's difficult and doesn't scale well unless you build redundant networks [145, 68, 144].

1.2  Computation as Transforming Representations

Our understanding of computation has changed significantly since the first practical electronic computers were built in the middle of the 20th century. The earliest applications of electronic computers involved running numerical algorithms and simulating physical processes relating to the design, deployment and defense against weapons of war. In the 1950s, the phrase information processing was employed to describe the sort of computing being performed by computers designed for commercial use. The term process is certainly appropriate given the dynamic character of computation, and it seems pretty obvious that computing operates on information in both the colloquial and Shannon sense of the word [151, 152].

By the waning years of the millennium, the phrase information process was being applied to both natural and artificial systems [11], but some argued it was too broad, encompassing as it does the transmission, transformation and storage of information. Moreover, it didn't seem that information really captured the essence of computing, leading some to suggest that it wasn't so much information as the representation of information that was transformed in carrying out computations [19, 18]. Peter Denning argued that (discrete) computation consists of controlled transitions among a sequence of representations [36], a characterization that can easily be generalized to apply to continuous computation.

In the context of biological systems, I prefer the simpler notion of transforming representations as it speaks to the nature of the underlying processes and provides a general framework for talking about how living organisms encode and utilize information about the past, present and future, and, in particular, represent their relationship with the physical world. Significant portions of the mammalian brain are devoted to maintaining dynamic representations derived from organized structure found in and on the animal's body and its immediate and extended physical environment. These internal representations serve to relate sensory experience to coordinates in the external world, and include retinotopic maps14 in the visual cortex, somatotopic motor-sensory maps15 in the somatosensory cortex, and entorhinal spatio-temporal maps16 located in the medial temporal lobe and acting as the primary interface between the hippocampus and neocortex. Any reasonably comprehensive account of biological computation must necessarily explain how these representations are generated, transformed over time in response to sensory input and implicated in behavior.

1.3  Language for Describing Neural Computations

As much as the spread-sheet and text-editor examples might convey the general idea of a mesoscale model, machine instructions and processor registers do little to illustrate how we might explain action potentials and local field potentials. Moreover, the sort of algorithmic account that makes sense for explaining smart-phone applications probably won't provide a particularly satisfying account of animal behavior. The language in which a theory is couched must be expressive enough to accurately and economically account for the relevant phenomena. Newton provided an adequate explanation for the elliptical orbits of the planets given observations from the best telescopes available at the time, but it wouldn't suffice to explain measurements made by the best modern instruments concerning hypotheses relating to quantum gravity. Explanatory models tend to be good at particular levels of detail and a mesoscale model is strategically located somewhere in the middle between micro and macro scales.

Writing programs for hardware based on the von Neumann architecture is simplified by a rich set of abstractions and tools. At the top of the software tool-chain are high-level programming languages like Java and C++ followed by optimizing compilers, byte compilation for interpreted languages, assemblers, linkers and loaders that produce or operate on intermediate representations including abstract syntax trees, byte codes, assembly language and machine instructions for each processor family. Together these intermediate representations constitute a hierarchy of abstractions that make sense to software engineers precisely because they were designed by engineers to help engineers deal with the complexity of modern software and computing machinery17

We need intermediate representations that speak the language of neural circuits, population codes, multiple sensory modalities, association areas, network topology, maps and embedding spaces that account for physical, behavioral and conceptual structure, e.g., retinotopy, all of which make sense to neuroscientists precisely because they were invented by neuroscientists to explain biological systems through the lens of the extant technologies designed to reveal relevant form and function at multiple scales spanning molecules, cells, networks, nuclei18, whole organisms and the ambient physical environments in which they exist.

1.4  Artificial Neural Networks for Modeling Biology

Algorithms written in conventional pseudo code or high-level programming languages provide a level of abstraction on top of the dominant model of computation, the von Neumann architecture. Most abstract models including Turing machines, finite-state automata, push-down automata, register machines and even parallel computing models including variants of the parallel random access machine (PRAM) model19 all reflect similar architectural foundations. Computations are characterized by relatively few, largely synchronous and predominantly serial threads of control carried out by centralized computing resources depending on a physically separate, contiguous random access memory (RAM) for storing instructions and data and requiring expensive fetch cycles to move operands and data back and forth between memory and central processing.

Neural architectures, both biological and artificial variants, can simulate the sort of computations that the von Neumann architecture excels at, but, on the whole, biological organisms are not very good at it20. Paradoxically, most programmers appear to be more comfortable with the single-thread-of-control model of programming emphasizing iterative, conditional and procedural abstractions. This preference is partly a consequence of the hegemony of the von Neuman's architecture, but is also due to the limitations of the neural circuitry imbued by natural selection.

Biological neural architectures depart from conventional computing architectures most obviously in terms of their utilization of many, primarily asynchronous, multiple-instruction-multiple-data (MIMD) parallel threads of control carried out by large numbers of distributed computing elements co-located with data. We generally don't think of biological networks as solving optimization problems, but both artificial and biological networks can learn to approximate optimal algorithms21.

Artificial neural network architectures along with the many specialized functions that can be realized as single-layer networks and combined to construct composite (deep) networks that provide a basis for modeling computations that transform one distributed representation into another. The class of possible such transformations includes both linear and non-linear transformations that allow for recurrent connections and can be shaped by a loss function to express sparse codes or perform regularization by adding noise. Neural network models can be trained by a variety of methods including back-propagation and Hebbian learning, two methods that are mathematically if not historically related [184] and possibly employed in biological networks [147, 125]. Given their computational expressivity, compositional versatility and intellectual origins in neuroscience, artificial neural networks provide a suitable framework for modeling biological neural networks that we exploit in the following sections.

2  Modeling Neural Computation

In this section we provide a high-level description of an artificial neural network that infers a mesoscale computational model from a combination of structural, functional and behavioral data. Later sections cover the details; the objective here is to describe the basic architecture of the model, its essential inference steps and the source of the data used for training and evaluation before embarking on a detailed description.

The term microcircuit has been used to refer to "functional modules that act as elementary processing units bridging single cells to systems and behavior" [62]. In this paper, we co-opt the term to refer to the complete (microscale) network of neurons within the neural tissue that we are attempting to model, and reserve the term functional module to refer to a portion or subcircuit of the complete network modeled as one component function at the mesoscale. For example, cortical columns might be treated as functional modules in a mesoscale model of the microcircuit corresponding to the primate visual cortex or glomeruli as functional modules in a mesoscale model of the olfactory systems of insects.

The basic problem of inferring the function of a neural circuit is often called functional connectomics [6, 139, 150] in recognition of David Hubel and Torsten Wiesel's use of the term functional architectures in describing the relationship between anatomy and physiology in cortical circuits [77, 76]. We begin with a brief exposition of the essential role that structural connectomics, encompassing the anatomical and morphological analysis of the microscale circuitry of neural tissues, plays in learning mesoscale computational models22.

2.1  Essential Role of the Microcircuit Connectome

If you were an engineer working for a leading semiconductor manufacturer and stumbled across a stack of micrographs—images generated by electron microscopy (EM)—revealing the 3D structure of the latest processor chip developed by your leading competitor, you might be reluctant to throw them away. A 5 nanometer resolution reconstruction of the chip based on these micrographs along with an understanding of how integrated circuit components, including transistors, are fabricated would be enormously useful in reverse engineering the processor.

Obviously this hypothetical scenario is not directly analogous to having micrographs of the sample of neural tissue you're interested in. For one thing, we don't know nearly as much about neurons and neural networks as we do about semiconductor chips. If you were trying to reverse engineer a chip, you could probably purchase or purloin one and experiment with it to understand how it works. Even so we do know a good deal about how neurons work and most neuroscientists would agree that the wiring diagram of the brain likely holds some clues about its function.

In the remaining sections of this paper, assume we have the following anatomical and morphological information about our target sample of neural tissue:

  1. a complete 3D reconstruction of all neurites in the tissue sample;

  2. the location of every synapse and cell body in the tissue sample;

  3. inferred cell type of every neuron based on location and morphology;

  4. the estimated strength of synapses based on size and vesicle count;

Given the above information, we can construct the static microcircuit adjacency matrix for the microcircuit connectome graph described in Figure 5 representing the connectivity of the microcircuit—at least to the extent possible given that the EM data represents a single snapshot in time and prior to imaging the tissue was subjected to the insult of being perfused, dehydrated, embedded in polyethylene and sectioned into thousands of thin slices. For example, if there are N neurons and A is an N × N adjacency matrix, the entry (Ai, j) in the i th row and j th column of A is 1 (Ai, j = 1) if there exists a synapse from the (putative) presynaptic neuron ni to the (putative) postsynaptic neuron nj with connection strength greater than some fixed threshold σ, and otherwise Ai, j = 0.

We can also define a sequence of related data structures called transmission-response matrices allowing us to combine the static information inferred from structural data with the dynamics apparent in the functional data. The transmission response matrix R is also N × N, but instead of a binary matrix, Ri, j is a scalar value between 0 and 1 that serves as proxy for the probability that, if an action potential propagates along the axonal arbor of neuron ni and there exist one or more synapses that connect ni to nj, then there will be a change in the potential of neuron nj, either positive or negative depending on whether the sum of the contributions from all the (shared) synapses is excitatory or inhibitory.

More precisely, the transmission-response graph Gt = { V, Et } at time t and its associated adjacency matrix RGt for a given microcircuit C are defined as follows: The set of vertices V corresponds to the set of N neurons { n1, ..., nN } in the microcircuit. There exists an edge (ni → nj) in the set of edges Et from a presynaptic neuron ni to a postsynaptic neuron nj if the activity observed in C during a specified interval of length τ ending at t leads to a firing of the postsynaptic neuron nj. The time-series of adjacency matrices { RGt | t  =  k × τ and 1 ≤ k ≤ T } of length T can be analyzed using techniques drawn from persistent homology theory [17, 87, 39] as demonstrated in Dlotko et al [37].

While there exist marginally better methods for filling in the entries in these matrices, their utility for our present purpose—learning mesoscale computational models—is limited by the quality and quantity of the functional data. Most of what currently counts as large-scale functional data consists of two-photon fluorescent microscopy with genetically encoded calcium (GECI) or voltage (GEVI) indicators expressed in the cell bodies and hence indicating the influx of Ca+2 at the axon hillock just prior to the initiation of an action potential propagating down the axonal arbor. The technology is improving rapidly—see here and here for competing commercial products, but the state of art is on the order of hundreds of neurons at 30 volumes / second or thousands of neurons at 3 volumes / second.

Calcium imaging hundreds or thousands of cell bodies is certainly better than most of the alternative technologiess—though multi-electrode arrays provide multi-photon imaging a run for its money. However, knowing the location and calcium flux of cell bodies is less useful than knowing the location and calcium flux of synapses. Much of the essential work of computation is happening in the synapses and an argument could be made that we should partition every neuron into subcompartments, the cell body being one such compartment that only differs in the details of how it communicates with other compartments, and treat the subcompartments as the indivisible units of neural computation. Once you can record from individual synapses, the relevant static graph structure is a directed multigraph in which any two edges between a pair of vertices are distinct from one another—also called a quiver in category theory—with neurons or compartments as vertices and multiple weighted edges corresponding to synapses between pairs of vertices.

Figure 5:  Here are three options for emphasizing local structure in the microcircuit connectome graph G: (a) neurons are the vertices of G, there is at most one directed edge in each direction connecting any two neurons—two neurons ni and nj often have both (ni → nj) and (ni ← nj), and the weight assigned to an edge between two neurons takes into account there being two or more synapses in a given direction; (b) neurons are still the vertices of G, however, each synapse and its coordinates in the microcircuit 3D embedding space are represented explicitly thereby revealing relevant local circuits even if the cell bodies are located outside of the region of interest—bounded by dashed horizontal lines in the above graphic, and G is now a directed multigraph; (c) each neuron is represented as a collection of compartments that comprise the vertices of G. The compartment boundary envelopes can be determined using criteria similar to those applied in large-scale simulations [107, 140].

The advantage of emphasizing synapses rather than neurons is that, unlike neurons, the locations of synapses often provide clues as to their function in a neural circuit. Since the real business of a neuron is being conducted in its synapses, the synapses of a sizable fraction of its functionally related neurons are likely to be co-located. Cell bodies can be located at some distance from their respective axonal and dendritric arbors along with their membrane-potential integration and thresholding apparatus and any centralized metabolic machinery or membrane manufacturing capabilities. There certainly are cell bodies studded with synapses—for example, motor neurons23 have been observed with hundreds of axosomatic synapses—in which case their locations are probably more likely to be indicative of their functions. Topological and graph-theoretical analyses of dense synaptic axo-axonic and dendro-dendritic microcircuitry yield highly discriminative signatures [28, 158, 56].

2.2  Learning From Functional and Structural Data

This section provides an overview of an artificial neural network (ANN) that learns a mesoscale model of an organism from a combination of structural (morphological), functional (physiological), behavioral and environmental data. To be clear, this model has never been built and hence neither trained nor tested. All of the network components (layers) have functionally analogous counterparts in applications of machine learning including computer vision, natural language processing, machine translation and automatic voice recognition. These counterparts lend no particular credence to the model described here, but may provide the reader with additional insight in understanding the proposed model.

The mesoscale model is also an ANN. To avoid ambiguity, we refer to the ANN that learns the mesoscale model as the model inference network, and the ANN that represents the mesoscale model as the inferred model network, using the abbreviations, inference network and inferred network, when the meaning is clear. The inferred network is an implementation and instantiation of the mesoscale computational model—the primary distinction being the same as the distinction between an algorithm and its implementation24. The inferred network is part of the inference network and we train both networks simultaneously, end-to-end using back-propagation and stochastic gradient descent.

More precisely, the mesoscale model is represented as a collection of interconnected and interdependent neural networks corresponding to functional modules as introduced earlier—see here. Each such module is modeled as a neural network comprised of smaller component networks—corresponding to the layers in a relatively shallow deep network—that are well understood in isolation, though often more complicated to understand when assembled into deeper networks. Examples of these component layers include divisive and contrast normalization, non-max suppression, max pooling and convolution with linear and non-linear filters with different receptive-field25 dimension and size.

The fact that the inference network includes the mesoscale model as a subnetwork—the inferred network—is no different than our using a more conventional machine-learning algorithm to learn, say, a nonlinear dynamical-systems model of neural function, or, for that matter, another machine-learning algorithm. Neural networks are machine-learning algorithms that just happen to be useful for modeling neural processes despite the fact that vanilla artificial neural networks are not at all like biological neural networks.

A mesoscale model requires [as input]:

  1. structural data: annotated connectome including cell types and synapse metadata as described earlier here;

  2. functional data: collection recording sites, their 3D embedding and associated recorded time series data26;

  3. behavioral data: behavioral and environmental recordings synchronized with the recorded functional data;

A mesoscale model defines [as output]:

  1. a family of possible configurable neural networks that correspond to instantiations of functional modules;

  2. a partition (possibly non-exact cover) of recording sites into (possibly overlapping) functional domains27;

  3. an assignment mapping each functional module to an instance of the family of configurable neural networks;

Alternatively, we might define a family of configurable neural networks as a set of functions—the set is called a basis and the functions basis functions—that together with a method of combining combining functions define a function space. In the most common case, every element of a function space is defined as a linear combination of basis functions. Informally, a sparse basis B for a function space F is one in which every { f ∈ F } can be approximated by a linear combination of basis functions such that most of the coefficients are zero. In the remainder of this paper, we use the terms "basis" and "family" interchangeably. The term "functional module" refers to a composite structure that includes a domain, interface and assigned network, appending the prefix "functional" or "functional module" as required when the occasion warrants more precision.

Figure 6:  A functional module is a member of a restricted family of multi-layer networks. Each such network is constructed from a small set of functionally well-understood—generally single-layer—component networks. Each functional module has a functional domain that consists of the time series data collected from a subset of the recording sites. Each functional module also has an interface that defines its inputs, outputs and dependencies with other modules. The term "functional network" is used interchangeably with "functional module" when referring to the network itself, distinct from the module's domain and interface. A mesoscale model is a set of functional modules whose associated functional domains cover the set of all recording sites, and whose collective behavior provides a mesoscale computational account of the target microcircuit.

Learning a functional module is analogous to setting the configurable parameters of a field-programmable gate array (FPGA) or programming an application-specific integrated circuit (ASIC). The progammer or field technician is constrained by having to work with a fixed allocation of modules implementing logic gates and supporting functions and forced to use an existing buss structure to combine the modules to implement the required behavior. Intuitively you can think of a family of configurable neural networks as a single network architecture that you (re)configure by adding feedforward (skipping layers) and feedback connections, bypassing layers, adding or subracting units in fixed increments. The more enabled layers, numbers of hidden units and recurrent connections all contribute to the complexity of the module.

Theoretically a network with only one hidden layer is already universal modulo the number of units, but the number of parameters, layers, recurrent connections, etc., make a substantial difference in practice. The (local) loss function includes a penalty term that is some function of the (structural) complexity of the configured functional modules. It should be possible to learn this penalty term given an appropriate training set.

2.3  Basic Mesoscale Inference Network Architecture

Figure 7:  This network shows the primary inference steps involved in learning a mesoscale model from functional and structural data. Each step is represented by a single layer. This is primarily meant for illustrative purposes. Some steps can be eliminated by exploiting existing knowledge and performing the required inference offline prior to training the network. Alignment is potentially one such step. Other steps are expanded and replaced by several substeps, each one carried out by one or more layers. Segmentation is an example of a step that requires multiple layers to implement. Finally, some steps are so interdependent that it makes sense to combine and interleave their operations.

Training and testing functional modules involves a complex optimization process to determine the size, shape and number of domains, the architecture of the component module networks and the interfaces that constrain their interdependencies. The inset reference to tensor (factorization) decomposition methods suggests one approach to learning functional networks that perform different computations depending on their context [186, 90, 122, 161, 170]. It seems plausible there exist functional motifs that serve as basic building blocks and appear in diverse nuclei throughout the brain, often repeatedly in regular patterns encoding topographic maps, for example, in the primary motor and sensory areas.

Here is a short description of the layers in the network shown in Figure 7:

  1. INPUT Structural data for reconstructing all the neuropil in the target tissue sample. The data consists of a stack of (2D) images obtained by serial-section electron microscopy aligned to provide a dense (3D) volumetric representation of the target. Functional data consisting of a series of (3D) volumes, each volume roughly the same shape as the structural volume. The data is obtained by two-photon fluorescent imaging or an equivalent technology.

  2. ALIGN Using fiducial landmarks identified on the structural and functional image data, the representative volumes are aligned so that each trace corresponding to the recorded calcium fluctuations of a single functional unit—neuron, synapse or compartment—has the same coordinates in each volume of the functional time series as well as the same coordinates of the corresponding morphological unit found in the single structural volume.

  3. SEGMENT The aligned functional and structural imagery is segmented into functional domains in a series of convolutional layers. In the process of doing so, a functional module is associated with each domain and instantiated as a network drawn from a restricted family of relatively-shallow, multi-layer networks. Segmentation boundaries are evaluated on the basis of how well the functional modules account for the local dynamics in their corresponding domains.

  4. INTERFACE The previous step along with this step and the two following are performed together in a series of convolutional and recurrent layers. The interface layers establish both local and distal functional dependencies between modules, sort out the inputs and outputs of each module including their valence—excitatory versus inhibitory, and evaluate (current) functional modules with respect to their complexity and predictive performance.

  5. CONFIGURE The domain, interface and network architecture of every functional module along with number of such modules is determined by the weights assigned to configuration parameters during training, using stochastic gradient descent. The architecture of the mesoscale model / inference network combined with multiple (local) loss functions reward predictive accuracy and penalize complexity measured in terms of network complexity and weight sparsity [185, 104, 186].

  6. DISTILL Several methods have been developed for simplifying complex neural network models consisting of many layers and ensembles of many networks [143, 72]. Often it is easier to learn a model that performs exceptionally well and use it to teach a simpler model to perform as well or better but at a fraction of the computational effort [52, 178]. This sort of two-stage training strategy may be useful in managing the trade-off between predictive accuracy and model complexity.

  7. OUTPUT The inferred network is a predictive model that maps neural recordings to observed behavior. In the case of the nematode worm (Caenorhabditis elegans) [30] or embryonic zebrafish (Danio rerio) [29] the most obvious behaviors with respect to locomotion include avoidance, chemotaxis, feeding, thigmotaxis and mechanisms of orientation are amenable to automated, high-throughput tracking and categorization facilitating training and testing [130]. Fly (Drosophila Melanogaster behavior) is somewhat more complex, but similarly well studied and automated [121].

2.4  Concessions Motivated by the Scale of the Data

For concreteness, assume the target organism is a fly (Drosophila melanogaster) or zebrafish (Danio Rerio), the microcircuit / tissue sample is the whole brain, and the organism has on the order of N = 100,000 neurons and S = 10,000,000 synapses. Let M be the number of microscale atomic computing units; these atoms of computation could be individual neurons or synapses, compartments or even small neural ensembles (nuclei) as discussed earlier here. Practically speaking, we don't want to create any data structures larger than M2. If we use compartments as the smallest unit of computation then the number of atomic computing units will be closer to S with most compartments representing at most a few synapses. In any case, the number of non-zero entries in the (sparse) adjacency matrix will be less than or equal to S whether M = N or M = S.

In theory, the mesocale model could be applied directly to the raw data. However, the structural dataset alone consists of a single volume corresponding to a cubic millimeter of fly or zebrafish neuropil and requiring on the order of a petabyte of EM micrographs to store. On top of that, the functional dataset consists of something on the order of 1000 volumes of super-resolution imagery, each volume requiring hundreds of megabytes to store, and the behavioral dataset in the case of the fly consists of many thousands of images taken by a high-speed optical camera—see here and here for example uses and relevant technologies—and requiring hundreds of terabytes, possibly as much as a petabyte of additional storage.

As a practical matter, all three of these data sources will have to be condensed. In the case of the structural data, we intend to make use of the microcircuit connectome to reduce the processing required during training and testing by several orders of magnitude. It is possible, that this attempt at efficiency will limit our ability to tease out subtle structural distinctions and thereby limit our ability to infer a suitable mesoscale model. For the time being, I expect we will have to live with this trade-off, given the alternatives. In the case of the functional data, as a first approximation, we will likely preprocess the data to extract calcium-flux rasters resulting in a considerable reduction in processing time for training and testing [40, 91, 120, 3, 2].

3  Functional Decomposition

This section focuses on a few of the most challenging problems needed to be solved in order to construct the inference network described in the previous sections and use it to infer a satisfying mesoscale computational model of some scientifically interesting organism. Given the complexity of these problems, some simplifying assumptions are in order. Regarding functional data, assume for the sake of discussion that the targets are genetically engineered flies (Drosophila melanogaster) expressing fluorescent protein calcium indicators (GECI) such as GCaMP6 [23] and that we can acquire nearly-complete coverage of all ~100,000 neurons and ~10,000,000 synapses at ~100 volumes / second in head-fixed flies. Similar protocols should work with embryonic zebrafish (Danio rerio). In discussing functional data, the term fluorescent point source (abbreviated point source) is employed to refer to the fluorescent trace of either a neuron or a synapse in the recorded image data.

Regarding structural data, assume the anatomical and morphological information described in Section 2.1, and the microcircuit connectome graph representation described in Figure 5.b in which G is a multigraph, the vertices of G represent neurons, there exists a weighted edge (ni → nj) for each synapse such that ni is the pre-synaptic neuron and nj is the post-synaptic neuron, and the coordinates of each axon and synapse are represented explicitly in the microcircuit 3D embedding space. Let U = { ui | 1 ≤ i ≤ | U | } represent the set of (putative) primitive computing units (abbreviated primitive units)—the set of all neurons and synapses as described in Figure 5.b—identified in the structural data, and W = { wi | 1 ≤ i ≤ | W | } represent the point sources. It is possible | U | ≠ | W | and almost certain that ui does not correspond to wi. Assume here for simplicity, that | U | = | W |.

The functional data is converted to a collection of trace sequences—one sequence of length the number of volumes in the functional data—for each point source. This requires tracking the signature fluorescent emissions for each source. The emissions associated with a point source are produced by a continually evolving set of calcium indicators, and so, in fact, the "points" correspond to small patches that change subtly from one volume to the next due to deformation of the tissue resulting from movement if the organism is free to move during recording or introduced by the software used to track point sources. The primary fluorescent emission site is in the cell body near the axon hillock in the case of neurons, and in the axon terminus of the presynaptic neuron in the case of synapses. Finally, the sequences are converted to time series of the estimated Ca+2 flux, dF = Δ F / F0, and dFt (w) denotes28 the estimated change in the Ca+2 concentration in the emission site of w at time t.

Let Q = { qi = ⟨x, y, z⟩ | 1 ≤ i ≤ | U | } be the coordinates of the (putative) primitive computing units identified in the fixed tissue sample, and P = { pi = ⟨x, y, z⟩ | 1 ≤ i ≤ | W | } the coordinates of the point sources in the functional data. By assumption, we know a lot about the elements of U. If ui is a neuron, then we know its type and synaptically linked neighbors. If ui is a synapse, then we know its pre- and post-synaptic neurons and their coordinates in the fixed tissue sample. For any two neurons ui and uj, we know all the synapses they share if any, including their direction, coordinates and some estimate of their strength. We know much less about W a priori, but there is much we can infer from looking at local patterns of functional activity to infer correspondences between subsets of U and W and by exploiting (vascular) landmarks common to both sources of data.

Our objective is to define a set of functional modules that together provide a computational theory of a given organism or functionally cohesive tissue sample. Specifically for each module we must define its:

  1. functional domain — for conciseness, when no confusion is likely to arise, we use the term "domain" to refer to the combination / union of what is technically called the domain (inputs) and range (outputs) of a function in mathematics textbooks29,

  2. functional network — since the term "function" is overloaded in computer science and computational neuroscience, we use the term "network" to refer to the instantiation or implementation of the (abstract) function associated with a given functional module, and

  3. functional interface — the theory includes a model of distributed computation involving the interaction of large numbers of functional modules and the "interface" of such a module defines the information flows between different, interacting modules30.

To achieve these objectives we need to (a) align the functional and structural data so as to assign specific functional activity to specific structural entities, (b) segment the now integrated functional and structural data into functional domains and determine the related functional interfaces, and (c) infer fully instantiated network architectures that provide a computational account of how activity at the molecular level gives rise to activity at the behavioral level. In lieu of a working model, any description of such a model is likely to be unconvincing except, possibly, to those few expert in the theory and application of all the component pieces. To make the presentation accessible to a larger audience, I've included descriptions of how we might achieve the objectives using a combination of conventional biological and computational technologies.

3.1  Functional and Structural Alignment

The task of alignment is to infer a bijection Φ : U → W that minimizes the distortion induced by the transformation Ψ : Q → P implied by Φ. As an analogy, suppose we have satellite images tiling an area of the United States taken when the area is in darkness and the only visible features correspond to the light produced by human technology. Our task is to create an accurate composite image by stitching the images together and aligning the composite image with a map that shows all towns and cities with populations more than a thousand, plus all federal- and state-maintained roads. The roads are sporadically visible in the satellie imagery from the headlights of traffic. This is the sort of problem that engineers solve every day in maintaining Google Maps and related geophysical services.

In this analogy, cities and towns are point sources in the satellite images corresponding cell bodies and synapses and the roads correspond to the vasculature of the brain consisting of arterioles (10-50 μm in diameter) and capillaries (5-10 μms in diameter) that supply oxygenated blood to the brain and the venules (7-50 μm in diameter varying dynamically) that return oxygen-depleted blood to the lungs and heart. These blood vessels or their fluorescent markers are present in both functional and structuraal data and can serve as fiducial landmarks to facilitate alignment.

In preparation for electron-microscopy (EM), the target tissue has to be stabilized using some form of fixation. This process generally includes eliminating blood from the vasculature since hemoglobin contains iron that can interfere with EM. The blood and extracellular fluid are generally replaced by a fixative, preferably so that the space occupied by the original fluids is preserved, since otherwise the tissue will be distorted and therefore more difficult to discern cell boundaries. Some degree of distortion is unavoidable. However, by labeling fiducial landmarks in the original tissue sample with markers that maintain their relative positions with respect to the features—synapses and cell bodies—we care most about, we can find correspondences between voxels from the in vivo functional recordings of the original pre-fixated tissue sample and voxels from the stacked EM imagery of the post-fixated sample.

Figure 8:  This graphic illustrates how a test stimuli might be used to help in aligning functional and structural data in the case in which we know something about the structure and function of some portion of the target tissue sample. In this case, suppose the sample is from drosophila and includes some portion of the medulla in the fly visual system covering a number of columns shown here as hexagons. The stimulus depicted in the graphic consists of a shadow moving across the visual field. We should expect to see autocorrelated features corresponding to a wave of activity in the columns with a period proportional to the rate at which the shadow is moving. We might use multiple trials in which the shadow moves in different directions to resolve ambiguity in the estimated correspondences or a less symmetrical stimulus in the same way one uses structured light to estimate the pose of the objects in a scene.

Figure 9:  This triptych describes the role of the parameter server. A multi-scale convolutional layer (c) applies a filter to a receptive field in its subordinate layer (a) resulting in a query to a distributed parameter server. The receptive fields of the filters and the corresponding queries to the parameter server are shown here as spherical regions. An instance of the server uses a replicated spatially-indexed database, depicted in (b) as a spill tree or KD tree, to extract the appropriate region of interest in a three-dimensional slice of the time series comprising the preprocessed functional dataset. The server then combines this functional extract with the corresponding subgraph of the microcircuit connectome graph, retrieved from a second spatial database, in order to generate a transmission-response graph Gt summarizing the state of the microcircuit at time t [37]. The convolutional layer can issue multiple queries in parallel, thereby applying multiple filters at multiple scales simultaneously. The parameter server is replicated on all of the machines being used to train or evaluate the distributed mesoscale inference network allowing a variety of highly-parallel processing protocols [1]. While the parameter server may seem a technical detail, its application here underscores the importance of the spatial structure of the data and the challenges involved in efficiently expoiting such structure.

Trading time for memory, much of the computational effort is performed offline by constructing spatially-indexed databases employed by scalable parameter servers [98] that answer multiple queries in parallel and return data structures generated on-the-fly that integrate preprocessed data with real-time computed topological and graph-theoretical features of the embedded data31. The parameter servers retrieve structured data extracted from three- and four-dimensional regions of interest corresponding to cubes, spheres and their temporally-extended counterparts. To simplify indexing, the coordinates of primitive computing units U and corresponding point sources W are reconciled so that for any i and j such that wj = Φ(ui) it follows that pj = qi, and all coordinates are scaled to the unit cube.

There are two spatially-indexed databases replicated across all servers. One embeds records of all synapses—contained in U—indexed by their reconciled and scaled coordinates. These records include fields for the pre- and post-synaptic neurons—also contained in U, their estimated connection strength, etc. Given a region of interest the server can reconstruct the subgraph consisting of the enclosed synapses and their pre- and post-synaptic neurons whether or not the neurons are located within the specified region. The other database takes a temporal index or range in addition to the three spatial indices so that, given the reconciled and scaled coordinates for any subset of W, it can retrieve the corresponding dF values from the relevant time series.

While the parameter server expects queries requesting the subgraphs fully contained in simple regions of interest such as cubes and spheres and their temporally extended counterparts, we don't expect that the subgraphs contained in these volumes will be functionally homogeneous. Rather, the regions of interest are intended to define limits on the span or locality of functional domains while the contained subgraphs define component circuits that may be parceled out to different functional domains. The synaptic circuits that comprise these subgraphs could be physically convoluted while their respective functions are computationally disjoint. This means that the basic operations that shape functional domains must operate on graphs, for example, graph unions, intersections, joins, complements and perhaps even products. In graph theoretic terms, the functional interface of a module is the set of edges, called a cut-set, that have one endpoints in each subset of a partition, called a cut, that divides the set of vertices into two subsets corresponding to the functional domain and its complement in the the microcircuit connectome graph32.

Figure 10:  Panel (a) shows the subgraph generated from the synapses in a centrally-located 20 μm sphere of the 7-column Drosophila medulla dataset produced by the Janelia FlyEM team [133]. The darker green nodes and black edges give some idea of just how complex the subgraphs are even in small volumes. This subgraph has 148 neurons and ~10,000 synapses. The simplicial complex consists of all k-simplexes for k > 0 where a k-simplex is a fully-connected subgraph — or clique — with k + 1 vertices in the unordered graph that has a single sink in the directed (network) graph. Panel (a) shows a 4-simplex with vertices highlighted in blue, the sink represented as a square and the rest of the vertices as circles, and the known cell types labeled in red. There are thousands of 4-simplices in the complex associated with this subgraph, typically with one of a few specialized cell types as sink. We construct feature vectors consisting of k-simplex statistics and topological invariants such as the Euler characteristic and Betti numbers, e.g., β0 is the number of connected components, β1 is the number of one-dimension holes, and β2 is the number of two-dimensional voids. Even relatively simple nearest-neighbor algorithms can cluster these feature vectors to reconstruct the layered, columnar structure of the medulla fragment. The graphic in panel (b) shows the result of applying K-means to the Janelia dataset.

Given such a subgraph and dF values for the relevant subset of U at some t, it is straightforward to generate the corresponding subgraph of the transmission-response graph Gt. Having combined the functional and structural data in a single data structure Gt, we can employ a subnetwork consisting of one or more convolutional layers designed to deal with structured data [123, 60, 154, 100]—graphs in this case—in order to parse data into component parts—functional domains in our case—in accord with an appropriate loss function accounting for predictive accuracy of the corresponding functional network. Alternatively, we might compute summary statistics of Gt and pass them along in a feature vector as illustrated in Figure 10 that we use to segment the graph and route the inputs and outputs, e.g., corresponding to afferents and efferents in the case of peripheral nerves, to layers that infer functional networks. The summary statistics map distinctive network motifs derived from the microscale to an intermediate-level representation — somewhere between the micro- and meso-scale — that are used to over-segment the microcircuit connectome graph into the graphical analog of superpixels [141].

In keeping with our promise to mention how conventional—not depending on artificial neural networks—methods might solve subproblems assigned layers in Figure 7. We consider the example methodologies and technologies drawn from neurobiology and machine vision, restricting attention to simple organisms with ~100,000 neurons, such as zebrafish (Danio rerio) and fruit flies (). The fruit fly is of particular interest due its extraordinary degree of inter-individual stereotypy in terms of neuron types, axonal projection patterns, neuronal activity patterns and synaptic connectivity [171]. While neither perfect nor universally applicable across all cell types [25, 27], this sort of stereotypy can be exploited to finesse some of our most challenging alignment and segmentation problems.

Biologists have bred tens of thousands of Drosophila variants, called GAL4 lines, that express the GAL4 gene in specific tissues. Combined with reporter genes that express fluorescent proteins, scientists can track specific neurons using confocal imagery. GAL4 lines have also been developed that express channelrhodopsin in specific neurons so that experimenters can turn these cells on or off to determine their role in supporting particular behaviors. GAL4 lines are employed to localize neural circuits responsible for behaviors. These tools have been used effectively to segment large brain regions into smaller subvolumes and create extensive maps of stimulus- and behavior-dependent activity [127, 183].

Researchers have exploited the stereotyped nature of Drosophila neural circuits across phenotypes in order to register brain images from multiple individuals, and then, using clonally-related clusters of neurons derived from the same neural stem cell that are functionally related—called neuroblast clones [15], they are able construct detailed maps that highlight functionally-specific neural circuits [108]. Scientists have also managed to register the brains of hundreds of larval zebrafish in order to construct anatomical maps featuring hundreds of brain areas associated with specific behaviors [137].

There is a related problem in machine vision that involves segmenting moving objects in video by identifying spatio-temporal volumes that span multiple frames of video, separating figure from ground in a stack of consecutive 2D video frames and then combining the resulting foreground fragments into a representation of the object's shape as it evolves through time. Fragkiadaki et al [41] propose a novel approach for solving this problem that is potentially relevant to the problem of bounding functional domains, and Januszewski et al [82] employ a similar approach to tracing neuropil in EM data that has produced state-the-art results on this demanding task.

There is a growing literature on using multiple-layer convolutional networks—with or without additional types of layers—in order to solve problems that involve parsing natural lanquage and natural scenes and then aligning images and text to generate image captions [89, 100, 88, 88, 154]. This task is related to the task we are interested in here, namely, segmenting structural data into functional domains using aligned (static) structural and (dynamic) functional data. These examples represent technologies that might be used to approximate, simplify or eliminate altogether the preliminary alignment and segmentation steps illustrated in the network shown in Figure 7.

3.2  Automated Functional Connectomics

How do you circumscribe a region of neural tissue or subgraph of the microcircuit connectome graph responsible for performing a particular function? One answer is that you don't, since it would appear that a single neuron can participate in multiple circuits, switching between circuits in a matter of milliseconds33. Moreover, depending on how you define "function" and "circuit", there can be more than one circuit per function. Artificial neural networks used in machine vision can already handle a certain amount of this sort of contextual variability. For example, in tracking people in video, a person's shape will appear to change as the person moves about, stoops to pick up a suitcase, or reaches to stow the suitcase in an aircraft overhead compartment. The functional relationships in which a person participates also change depending on context as in the case when a person enters or exits a car, picks up or sets down an object, dons a coat or removes his or her shoes. Networks developed for natural language processing can learn relations that are expressed using similar words but have different meanings depending on the context in which they appear [8, 112, 160, 16].

Actually, I don't believe individual neurons or subcellular compartments play an important mesoscale computational role in any functions. Rather, I expect there is great deal of redundancy present, not so much in order to deal with accident-, development- or senescence-related cell death, though admittedly these factors ultimately do have a significant impact on computation, but simply to make computations more stable and reliable34. An ensemble is typically defined as a group of neurons that exhibit spatiotemporal co-activation. If such entities exist, persist for a reasonable length of time and recur periodically, then a DRNN should be able to infer an activity signature suitable to detect their appearance and track their evolution over time. Using such signatures, we should also be able to estimate ensemble boundaries even if they appear somewhat ephemeral when observed over shorter time spans. As for inferring a function realized as a confederation of ensembles, the set of DRNN models is certainly powerful enough to learn most any reasonably well behaved function one could imagine. The goal isn't simply to reproduce the input-output behavior of an ensemble, but to do so by abstracting from the apparent component complexity and emphasizing the composite reliability35.

I think it would be hard to prove that the brain can't be decomposed into parts. The problem of finding a satisfying decomposition is that not all modes of information passing are local and point-to-point. Even an integrated circuit has information pathways besides the conductive traces purposely etched into the semiconductor substrate36. It is possible that neural computation is crucially dependent on a very different model of information processing than we are familiar with. For example, a model along the lines of crowd-sourcing, involving a collection of relatively simple, self(ishly)-motivated, semi-independent agents loosely-organized in constantly emerging, evolving and dissolving coalitions, exhibiting collaborative, competitive and adversarial characteristics and using simple distributed protocols for resolving conflicts such as voting, polling, markets, auctions, etc.

The characteristics of functional domains fall into several categories: geometric: location, neuropil density, volume; functional: redundancy, implementation variability; relational: overlap with and interface to neighboring domains; computational: persistent state, sequence processing, recurrent (intra-layer) and feedback (inter-layer) connections. However, if we design the learning architecture properly, these characteristics won't have to be explicitly accounted for in the model, but rather will emerge during training. That said, the architecture probably won't have to be particularly novel; the loss function — likely a composition of several component loss functions — will shape the model. Some features common in machine vision and natural language processing applications will likely play an important architectural role, e.g., convolutional layers with different scales / sizes of receptive fields in combination with a sparsity penalty, e.g., using an L1 norm to constrain functional assignments will allow for multiple overlapping domains involving functions that consist of multiple circuits, and circuits that contribute to multiple functions.

Figure 11:  This figure extends the network layers illustrated in Figure 9 to include the first stages of the inference network responsible for learning functional modules. The circle shown in panel (a) looking like an unimaginatively conceived mandala represents the interface between a functional module and its neighboring modules. Each of the small red circles represents a primitive computing unit—synapse or cell body—corresponding to a source of information flowing into or out of the circuit. The transmission-response graph Gt at time t encodes information about the initiation of an action potential at an axon hillock or the transmission of a signal across the synaptic cleft occurring in the τ-duration interval starting at t.

Since Gt only reports on events relating to the propagation of action potentials, we need some other means of updating the units that aren't the sites of such events. This requires dynamically adjusting the state of the interface neurons to compensate for impedance mismatches between communicating functional modules, and routing information to the input and output layers of the functional network, the units of which are depicted in panel (c) as green and blue circles, respectively. This dynamic coupling is achieved by adjusting the weights of a complete-bipartite-graph layer with recurrent connections shown in the inset in panel (b) trained along with the rest of the functional module's network shown in the inset in panel (c).

Figure 12:  This graphic depicts two spherical subvolumes—labeled (a) and (b)—representing functional domains covering portions of two separate arbors of a drosophila medulla intrinsic neuron (Mi1). Each domain intersects with other neural processes—not illustrated here—resulting in complex synaptic circuits circumscribed by each domain. The two spherical subvolumes are disjoint but their respective functional domains are connected by the Mi1 process labeled (c) in the graphic.

As illustrated, this process may intersect several other functional domains between (a) and (b) but makes no synaptic connections with these intervening domains and hence is effectively invisible to the graph-theoretic analysis of the subgraphs embedded in subvolumes (a) and (b). The connectome graph makes it possible to efficiently identify both local—spanning a few tens of microns—and longer-range dependencies—spanning hundreds of microns.

The 3D embedding of the connectome provides both the local circuitry—distances measured in terms of a few tens of microns, as well as longer-distance connections spanning hundreds of microns. This is important since the local filters (kernels) that implement convolutional layers will have receptive fields whose size is a small fraction of the size of the entire volume. The connectome allows us to exploit two complementary notions of functional dependency: spherical subvolumes of the 3D embedding enclosing subgraphs whose structure determines local circuits, while the connectome adjacency matrix determines longer-range dependencies between these local circuits as illustrated in Figure 12.

4  Learning Mesoscale Models

This section explores two illustrative architectures for designing the mesoscale-model inference network. Following additional discussion concerning microcircuits and modules that will come in handy later in this section, we describe a simple variant of the mesoscale modeling problem and propose an network architecture for inferring such a model. In this simple variant, we assume that some combination of the techniques for identifying functional domains work described in the previous section will work well enough to segment the microcircuit into a set of functional domains. The principle remaining problem in this case involves assigning a functional networks to each domain, and so we present a network architecture and discus its advantages and disadvantages.

Building on the architecture for this simple variant, we dismiss the assumption and formulate an alternative architecture designed to infers a covering set of functional modules including their domains, thereby solving the original problem of inferring a mesoscale computational model from functional and structural recordings. The illustrations that accompany the prose in the following sections are meant to be suggestive rather than proscriptive. There are likely many instantiations of the ideas presented in this paper, including variations in the network architecture, different loss functions, alternative training protocols, etc. The point of this paper is to lay out a general framework, introduce some useful concepts and terminology, and solicit suggestions for datasets to test these ideas.

4.1  Microcircuits and Modules

Assume the fluorescent point sources and primitive computing units are aligned as discussed, so that every vertex in the microcircuit connectome graph G = ( V, E ) is associated with a dF time series. Recall that a functional domain is a subgraph of G. The interface of the associated functional module is defined by the smallest set of edges—cut-set—separating the module subgraph from the rest of G. Suppose Gm = ( Vm, Em ) is the subgraph associated with module m, Im is the module interface, and Cm is the cut-set defining the Im. If (vi → vj) ∈ Cm, then either vi ∉ Im or vj ∉ Im. Conversely, if vi ∈ Vm, and (vi → vj) ∈ Cm or (vj → vi) ∈ Cm, then vi ∈ Im. Figure 13 describes how a loss function might constructed to encourage the properties we expect in a mesoscale computational model.

Figure 13:  The graph shown in the large circle—outlined in solid black—on the left represents the full microcircuit connectome graph and the enclosed circle—outlined in dashed red—represents the domain of one functional module. The inset on the right depicts the functional network associated with the inscribed module. The mesoscale model combines the functional networks associated with the model functional modules into one large recurrent network. In the simplest arrangement, this composite network takes sensory patterns as input and produces activity patterns as output.

The loss function includes two terms relating to prediction accuracy: One term measures how well the model as a whole reproduces the recorded activity given the associated sensory input. The other term measures the ability of the individual functional networks to reproduce the activity observed in their respective functional interfaces. The second term is offset by a third term in the loss function that penalizes the complexity of functional networks calculated as a function of the number, size and type of their component layers. The combined second and third terms constitute a proxy for explanatory value.

Neither circuits nor domains are defined entirely by their enclosing volumes. More than one circuit can occupy a volume. If V1 is the volume containing circuit C1 and V2 is the volume containing C2, then it is possible that V1 ∩ V2 = ∅, V1 ∪ V2 = V1, V1 ∪ V2 = V2, etc., treating the volumes as closed sets. Circuits are represented as directed graphs and so their edge and vertex sets could overlap if we allow that circuits can be functionally reconfigured to play different roles. A circuit can participate in more than one function. This could be because the decomposition into functional domains allows multiple interpretations or because the circuit dynamically reconfigures itself so as to play a different role in its current functional domain assignment or to play a role in another functional domain. If the circuit contributes to multiple functions either simultaneously or serially, then it may make more sense to represent the circuit as a separate functional domain composed of exactly one circuit.

What are the component circuit functions? How are circuits informationally dependent on one another? How much does locality matter and how are short- and long-distance connections different from a computational perspective? Changes in circuit function may occur under the control of genetic, metabolic or cellular-signal-transduction pathways. These biological pathways serve essentially as wetware programs to control the expression of proteins, the production and distribution of energy in the form of ATP, diffuse neuromodulation and synaptic transmission. Their operation will remain hidden from us until such time as we are able to label and image the relevant markers along with the markers that serve as our proxy for local field potentials.

What use is the connectome in functional analysis? Perhaps the most important service the connectome can render is to constrain the size and complexity of functional interfaces, and help to determine functional dependencies. Having the static circuit wiring diagram simplifies collecting together the possible inputs and outputs. Once we've defined these functional interfaces, we have some confidence that our machine learning techniques will be able sort out the dependencies and route information as required by the local circuitry, but first we have we have to understand the underlying biology well enough and develop technologies subtle enough to record and quantify the relevant information.

Figure 14:  The above graphic depicts a sequence of functional recording frames: { ti : 0 ≤ i ≤ 3 }. This example illustrates some subtleties that arise in working with graph embeddings and embedding-space volumes. We use the concept of the minimal convex spatial envelope (MCSE) of a graph as discussed in the main text to illustrate the issues and refer to a (neural) circuit and its corresponding subgraph in the microcircuit connectome graph interchangeably. Each frame in the graphic shows three circuits: C1, consisting of { a, b, c, d, e }, with its MCSE outlined in green, C2, consisting of { f, g, h }, with its enclosing volume MCSE outlined in red, and C3, consisting of { f, i, }, with its MCSE outlined in black.

Note that C1 and C2 are disjoint despite the fact there corresponding MCE volumes overlap. In the sequence, e, which is presynaptic to d and f, activates the postsynaptic neurons d and f. Propagation from e and f then continues independently. Should C1 and C2 belong to the same functional domain? It seems more likely that C3 and C3 belong to the same functional module. Note that all three circuits are highly correlated and so, if we believe correlated activity is an indication of united function, then all three circuits would contribute to a single function.

4.2  Plan I: Finessing Functional Domains

In this case, we apply one or more of the techniques for identifying functional domains and then dedicate a configurable functional network to each domain, using a cover rather than tiling to allow some flexibility sorting out the outer boundaries of the functional domains. Given the functional domains we dedicate a configurable network to model each functional module, perhaps assuming a functional-domain cover of the connectome graph vertices—corresponding to aligned primitive computing units and fluorescent point sources—rather than a tiling to allow some flexibility around the boundaries of the functional domains. While this approach is conceptually simple, it relies heavily on our ability to accurately identify meaningful functional domains [ … ] the domains cannot be substantially altered to account for the limitations of the functional network [ … ] we can't easily identify repeated functions and hence the basis is under-constrained [ … ] Figure 15 [ … ]

Receptive fields for the convolutional layers depicted in Figure 7 are simple, convex 3D volumes such as cubes or spheres. This is done to simplify covering the entire volume and facilitate retrieving subvolumes of the connectome embedding corresponding to parameter-server queries. These compact receptive fields do not imply that the model only accounts for short-range connections enabled through adjacent or overlapping subvolumes. As pointed out in Figure 12, the connectome adjacency matrix records possible dependencies spanning the entire volume. The maximal subgraph enclosed by a given subvolume need not be connected, and could be empty if there are no synapses in the corresponding region of tissue. The smallest convex subvolume enclosing a given subgraph [ … ] we refer to this as the minimal convex spatial envelope (MCSE) for a given subgraph [ … ] convolution filter kernels ranging over multiple scales [ … ] the configuration layers and related terms in the loss function are capable of inferring arbitrary functional domains as long as they fit within the receptive field of some filter in the model functional basis [ … ]

Figure 15:  The above graphic depicts a simple variant of the mesoscale-model architecture shown in Figure 7. The important simplification results from the assumption that, independent of the mesoscale model, we can infer, to a reasonable approximation, the functional domains of the modules that comprise the model. We allow some overlap in the functional domains to account for uncertainty regarding their extent or overlap that arises from context-sensitive circuitry shared by multiple modules, assuming that too is understood well enough for us to make an informed guess. This simplification allows us to assign a dedicated configurable functional network to each domain, an architectural advantage we can't avail ourselves of in next model (Figure 16) in which we have to infer the number of modules and the extent of their associated domains. The items numbered I through VI are referred to as levels and are likely to be realized as multiple layers in any implementation of these ideas.

Given the functional domain boundaries, the associated interfaces depend only on the microcircuit connectome graph. The inferred network proper corresponds to the darker green units in shown in Levels II, IV and V. The model assumes a single functional-network architecture replicated for each module, shown in the figure shaded a lighter green in Level IV and partially occluded by the darker green configured network determined by the parameters in Level III. The loss function depends on the difference between the observed (Level I) and predicted (Level VI) point-source values at t + 1 and on the configuration parameters in Level III that determine for each module the number and type of layers as well as their size / number of hidden units. Level I features derived from the microcircuit subgraphs that define functional domains provide clues relating to structural motifs that can be exploited during training by the configuration Level.

Figure 16:  The above graphic builds conceptually on the network shown in Figure 15, dispensing with the simplifying assumption that, independent of the mesoscale model, we can infer the functional domains that comprise the model. Levels IV and VI have been modified and Level VII added to enable us to learn the functional domains as part of the model. The Level IV fixed modules in Figure 15 have been replaced by a convolutional layer and (unconventional) filter bank, consisting of K filters, that provides a functional basis, F = { fk | 1 ≤ k ≤ K }, for the space of functional modules.

This basis spans multiple scales and multiple network architectures. It is intended to be sparse in the sense that any module (network) can be realized as a linear combination, h = ∑Kk = 1 (wk × fk), of a small number of basis functions (networks). This implies that only a few of the coefficients (weights) in the linear combination are significantly different than zero and so only a few basis functions contribute in defining any given functional module. A sparsity-inducing term in the loss function such as an L1 or mixed L1 / Lq norm is employed to control sparsity.

Several of the layers in the mesoscale model are unconventional in that they do not correspond indexed array or matrix object. Instead these layers correspond to coordinate spaces embedding functional and structural data or their inferred products indexed spatially and accessed using variants of the distribute parameter server technology introduced in Figure 9. In performing convolutions, the conventional sliding-window is replaced by parallel addressing scheme operating on a 3D grid of points spaced according to a stride parameter and spanning the relevant embedding space.

Each filter has separate Level 3 configuration parameters for each point in the embedding space as well as separate Level VI prediction registers in which to store results. Levels III and VI are divided into compartments for the purpose of keeping track of this information. The dashed red lines dividing Level III and Level V into four subcompartments each are meant to illustrate the (unrealistic) case in which K = 4. There are as many bases in the model functional basis as there are filters in the filter bank, notated K in the graphic above. The net result is that there are many fewer bases than there are functional modules and so we expect that the model will converge on a set functional motifs representing components that are broadly replicated and applied.

Level I plays an even more important role here than in Figure 15 since in addition to providing clues useful for constraining functional-module networks, Level I features are also expected to provide features useful for determining functional domains. Since a functional domain is nothing more than a subgraph of the microcircuit connectome graph together with a map from vertices to fluorescent point sources, it stands to reason that the graph-theoretical and topological features encoded in Level 1 would be relevant if function follows form and the corresponding two datasets are spatially aligned.

Figure 17:  This graphic illustrates how the functional basis filters decompose the connectome graph and associated point sources into functional domains. Each of the large dashed and solid circles represents a spherical subvolume of the connectome embedding space. When training is complete, each subvolume and each point source will be claimed by exactly one basis filter. In the graphic, three color-coded filters are shown claiming a total of six of the fourteen subvolumes. The stride of the sliding-window convolutional operator is half of the diameter of receptive-field subvolume. Note that with the exception of B none of the filters include—and thus are responsible for modeling—all the point sources in their subvolumes.

Figure 18:  This diagram represents the multi-level layer encoding the location-specific configuration parameters for the mesoscale model. Each filter f in the functional basis has a level allocated to storing those parameters of the functional module that govern the local properties of the module. Each column μ of that level has a set of parameters { π } that are specific to each location in the 3D grid of locations that determine the receptive fields—and their associated maximally-enclosed subgraphs and corresponding point sources—employed in performing convolutions. These properties include the enumeration of those point sources that the functional module has assumed the responsibility of accounting for with its network. The local properties also include the parameters of the local impedance matching and I/O sorting network embedding layers. They don’t include global information about the number, size and type of layers that comprise the module network nor do they include the parameter values that define those layers.

Figure 19:  The functional-module configurable network is determined by a set of basis filters each of which has one set of (global) parameters (A) that is the same for every location in the 3D grid spanning the connectome embedding and a second set of parameters (B) that defines location-specific properties and was described in Figure 18. The global parameters determine the number, size and type of layers using sigmoidal switches that change the number of units within a layer in fixed increments, eliminate layers altogether by enabling pass-through layers, add recurrent and skip forward edges, select between half-wave rectification, divisive normalization, max pooling, logistic and other activation functions. Since there is only one fully configured network for any given filter at any particular time, we have added what we refer to as an impedance-matching embedding layer (C) specific to each location in the 3D grid that spans the connectome graph embedding space. This layer also accommodates variation in the size of the learned location-specific subgraph that defines the functional domain of the basis filter and was described in Figure 17.

Figure 20:  Building on Figure 19, here are a couple of examples of configurations that handle special cases and degenerate subgraphs. If the functional domain of the configurable module for a given basis filter has no assigned point sources in a given location, then the filter is not relevant in that location and would not, in any case, be selected to contribute to calculating the (global) loss. If the the domain does contain one or more point sources, but the corresponding (embedded) subgraph has no edges, then the input equals the output and the function is configured as a simple pass-through by enabling the connection labeled (B) in the graphic. In the case that the functional domain represents one or more synapses that are otherwise not connected with one another, then the best model might be simple linear transformation (A) and the output interpreted as an estimate of synaptic weight.

Figure 21:  This graphic combines the components from Figures 17, 18 and 19 to illustrate how signals measuring the predictive performance of functional modules are fed back and combined additional with local network features to assign cells to functional domains. These features (not shown) are derived from the local properties of the static connectome graph and summary statistics of the functional time series characterizing the mutual information of adjacent subcircuits. A is a multi-layer network that learns how to apportion cells to functional domains. B adjusts location-specific configuration layer entries and C uses this updated information to restrict functional-module domains accordingly. The inset graphic underscores the fact that functional domain assignments often involve restrictions with the dashed red lines depicting cells that are not included in the domain.

The aligned functional and structural datasets constitute a high-dimensional multivariate time series informed by a static 3D embedding and complex network structure and latent dynamic functional dependencies. Generally, the phrase "high-dimensionality" is applied to problems with hundreds or thousands of variables, while we are primarily concerned with problems having hundreds of thousands of variables or more. Ignoring the added complexity of accounting for diffuse modulatory signaling pathways, the microcircuit connectome graph significantly limits the number of direct functional dependencies that we have to deal. However, imputed small-world properties of biological neural networks renders this observation small comfort [115, 157, 131, 163].

You can decompose a multivariate time series by chopping it up into shorter-length time series that are segments of and have the same dimensionality as the original series. Alternatively, you can group together variables to construct a new time series the same length as the original, but of a lower dimension, corresponding to the number of groups. In many cases, neuroscientists do both; for example, spectral methods are used to reduce the dimensionality of calcium imaging data by computing principal components or performing singular value decomposition and then various segmentation algorithms can be applied to identify segment boundaries, aligning segments with observable recurrent behaviors that appear in the series [91, 2].

Many of the most relevant methods can be characterized as some form of regularized multivariate regression [69]. There is a great deal of related work, including important contributions by Leo Breiman, Jerome Friedman, Trevor Hastie and Robert Tibshirani, along with a growing toolbox of powerful algorithms including matching pursuit [102], projection pursuit [42], LASSO (least absolute shrinkage and selection operator) [174] and related methods. Also relevant are insights from computer vision and spectral graph theory on solving perceptual grouping problems using eigen-decomposition methods [182, 155].

Aapo Hyvarinen developed a generalization of projection pursuit for time series designed to identify projections of time series that have interesting structure as defined by Kolmogoroff complexity or coding length [79]. It might be worth mentioning work by [67] involving a combination of PCA, temporal correlation and Bayesian segmentation using variational, non-parametric and Markov Chain Monte Carlo (MCMC) derived methods. Perhaps also one of the more recent papers on block-variable selection applied to biological times series [101]. Also warranted is some mention of Granger causality [58], its application in analyzing neural recordings37 and the relative merits of its linear and non-linear variants [14].

Several of the best known algorithms involve solving convex-optimization problems, generally using gradient-descent methods of one sort or another. While finding the optimal solution is intractable in large part due to the method of regularization, efficient approximation algorithms exist that alternate between solving two minimization problems with disjoint sets of variables, holding the first set of variables fixed and solving for the second set and then reversing the order fixing the second and solving for the first [20, 31]. Solving such problems within the context of artificial neural networks can be accomplished with an L1 loss and logistic (sigmoidal) activation function. It is perhaps worth noting that many of these algorithms are unsupervised.

Figure 22:  In the simplest case, each point source μi is assigned to exactly one functional domain—that is, one basis filter in one location in the 3D grid of locations. There are relatively few receptive fields that can contain any given point source. The number depends on the resolution of 3D grid which depends on the size (diameter) and shape (spherical) of receptive fields and step size (stride) of the sliding-window convolutional operator. For a given point source μi, let's say there are R possible locations and F basis filters, the set of possible functional domains Di is of size H = R × F = | Di |. Domain asignments are learned during end-to-end training using one of several methods including winner-take-all network, max pooling layer or a softmax layer combined with a gating mechanism similar to the error carousel used in Long-Short-Term Memory recurrent-network (LSTM) models [148, 73]. The graphic shows one point source with H weights followed by a softmax layer and then a generic gating function. To support hyotheses allowing for context-dependent domain adaption, the bottom layer—shown as a pass-through in the figure—could be replaced by an LSTM hidden layer. [...] this needs either more or less detail to be useful [...] note that sparse coding is neither efficient nor desirable in this case [...] alternatively one can factor the model38 [...]

Figure 24:  [...] This graphic extends Figure 18 [...] the configuration layer sub-region labeled f* assigns a filter-location-specific scalar value (weight) in the unit interval to each basis filter thereby determining a linear combination of the basis filters at each location [...]

Figure 25:  This figure39 builds on Figure 13 by providing detail on how the sparse functional basis is trained. In the following, the Ai assign point sources (cells) to functional domains, the Bi indicate basis filters and their corresponding functional networks, the Ci constitute local cost / loss functions, the Di corresponding to forward-propagating mux (multiplexer) / backward-propagating demux (demultiplexers) units, and E is the global loss comparing predicted and observed output. Three basis filters {f1, f2, f3} and their associated functional modules {B1, B2, B3} are shown. The graphic illustrates the application of these three filters to the spherical subvolume corresponding to the receptive-field centered at location μi.

The functional interfaces for the three filters are shown using the same graphical conventions introduced in Figure 21, specifically, the network components {A1, A2, A3} that assign point sources to functional domains and the origin of their parameters in the filter-location specific regions of the configuration layer. Note that in this example all three of the interface components Ai receive input from the same point sources. The graphic focuses on how the basis filters are evaluated at location μi, how values obtained from different filters at the same location compete with one another to account for the module-level predictions at that location, and how values obtained from two different locations μi and μj are combined to generate predictions for entire model. Not shown are the sparsity-inducing components that ensure each point source / cell is assigned to exactly one functional module domain.

To reiterate and emphasize key points from earlier figures, each filter has a set of location-filter-specific parameters that encode a local impedance-matching embedding and serve to determine its functional domain at each location by restricting the set of point sources / vertices that constrain the local maximally enclosed subgraph of the connectome graph, i.e., the spherical subvolume that constitutes the receptive field centered at 3D grid location μi in the microcircuit-connectome-graph embedding. The configuration layer sub-region labeled f* assigns a filter-location-specific scalar value (weight) in the unit interval to each basis filter thereby determining a linear combination of the basis filters at each location. Two loss functions are shown: a local loss that minimizes the reconstruction error of each functional module in predicting its outputs from its inputs and a global loss that accounts for all of the outgoing / efferent / behavioral output. Not shown is the sparsity-inducing term in the global loss that ensures for any given location that the weights of the corresponding linear combination of basis filters are mostly zero.

It will be some time before we can optically resolve and accurately record from each synapse in a fly or zebrafish, much less a mammal—the etruscan shrew is the smallest known mammal by mass and has about 10,000,000 neurons in its cortex alone which is just about the same number of synapses in a fly40. Suppose we are given the complete microcircuit connectome graph G = { V, E } and related metadata as described in Section 2.1. For a subgraph Gm = { Vm, Em } such that Em is defined by the set of synapses retrieved from a given subvolume and Vm is the set of all neurons such that v ∈ V if and only if either (v → w) ∈ E or (w → v) ∈ E for some w ∈ V where w can be located outside of the minimal convex spatial envelope of Gm.

How much could we learn about the function of the neural circuit corresponding to Gm given the morphology and cell type information available in the connectomic data and the activity recorded from each cell body corresponding to a neuron in Vm? Perhaps quite a lot given a sufficient amount data spanning the behavioral repertoire of the animal model [93, 116, 38, 3, 2]. While we can't take advantage of the functional motifs apparent in the time series of transmission-response graphs, we can exploit the structural motifs inherent in the static connectome graph. It would certainly be worth trying to learn edge weights for option (a) in Figure 5 and possibly even the individual synaptic weights for option (b) though that would be challenging.

Appendix A: Technical Vocabulary

Appendix B: Connecticomic Terms

A1 — A point cloud is a set of data points embedded in a coordinate system (typically three-dimensional) used to represent the external surface of an object or points of interest within a spatial envelope. In our case, the points correspond to the recorded fluorescent emissions from genetically encoded indicators of activity in cell bodies, synapses or other locations of neural activity. A series of such functional point-cloud volumes is used to represent the activity of a neural circuit over some experimental time interval.

A2 — A connectome graph G represents a neural circuit as a set of vertices (typically) corresponding to neurons and edges (typically) corresponding to connections between neurons and representing synapses. G is generally static representing a snapshot of the circuit at a particular time. G is embedded in a 3D volume corresponding to the geometry of the tissue sample from which the connectome was generated. A transmission response graph is a connectome graph in which each edge is weighted by the strength of its connection estimated over a (typically) short fixed interval of time.

B1 — An input-output encapsulated microcircuit is a functionally-closed biological system consisting of an isolated neural circuit with its (only) input corresponding to environmental stimuli and its (only) output corresponding to behavioral responses, such that the latter can be reproduced from the former from an (computational) model—referred to as a closed-loop transfer function in the control-theory literature—of the underlying dynamical system.

B2 — In the sequel, we present a class of models such that each model is constructed from a set of functional modules [62, 129, 63, 24] each of which covers a spatially/geometrically-restricted functional domain of application and endeavors to predict the state vector summarizing its domain of application at time t from a preceding contiguous temporally-ordered sequence of such state vectors. Each functional module is realized as one of a restricted class of configurable convolutional networks.

C1 — A spatially-localized synaptic-circuit (SLSC) corresponds to a graph constructed from the set of synapses in a (typically spherical) subvolume of the embedded connectome graph such that the edges correspond to the synapses and the vertices correspond to the pre- and post-synaptic neurons of each synapse whether those neurons are located inside or outside of the subvolume. Technically this is multi-graph since for any two vertices there can be multiple connecting edges in each direction, typically having labels distinguish them. The receptive fields of the convolution filters referred to in E exactly span such spherical subvolumes. The graphic shown corresponds to the SLSC generated from a spherical subvolume approximately 30 μm in diameter extracted from the central column of the Janelia drosophila medulla seven-column connectome dataset.

C2 — A topologically-invariant graph-embedding reconstruction (TIGER) maps each point in a 3D grid of points spanning the volume in which a (directed) graph is embedded to a vector of topological-invariant properties computed for the SLSC centered at that point. The width (diameter) and stride (distance between points) of the SLSC determine the number and layout of points and their corresponding vectors. The resulting vectors are classified (typically using nearest neighbor methods) and the SLSC corresponds to the 3D grid of (class) labels shown color coded in the graphic. For more information, you might want to look at the analysis in this Jupyter notebook.

D1 — The intuition guiding our emphasis on spatially-localized synaptic-circuits is that synapses are the primary loci for computation and their proximity to one another provides important clues as to their collective behavior and underlying function. Of course, this isn't quite true since the entire cell membrane, studded as it is with ion channels and traversed by legions of transport molecules, participates in the computational processes conducted by neurons. It's worth pointing out that it is only through the use of the connectome and its related metadata that we are able to (a) identify the synapses in a given subvolume and (b) work our way back to include all the relevant pre- and post-synaptic neurons.

D2 — An SLSC is defined by the synapses contained in its target spherical subvolume, but the resulting graph is not fully contained within that volume since the vertices of the graph correspond to all pre- and post-synaptic neurons. This graph showing two spherical subvolumes is meant to underscore this consequence of the definition by illustrating how the connectome graph allows us to determine both short- and long-distance connections.

E — This graphic shows the architecture of the mesoscale model sans the layers responsible for aligning the functional and structural data. Our model relies on the use of a sparse functional basis (SFB) to discover functional motifs in the microcircuit. These repeated subunits constitute the building blocks for mesoscale models. Not only do they represent anatomically similar subcircuits such as the columns in the visual, auditory and somatosensory areas of the mammalian neocortex, but we expect similar subunits find common application in diverse nuclei throughout the brains of organisms from finches to flies. When talking about (artificial) neural network architectures, we use the term "receptive field" in accordance with its usage in convolutional neural networks41, and the terms "basis" and "filter" with respect to the literature on sparse coding with the caveat that the basis filters, referred to as functional module basis filters, follow mathematical conventions for function spaces.

Our use of (artificial) neural networks to represent (real) neural network circuits is apparently controversial with some neuroscientists. The argument in favor hinges on the fact that despite rumors to the contrary, well-engineered neural networks are composed of relatively simple, mathematically well-understood components, including convolutional and max-pooling layers, divisive normalization, and sigmoidal and logistic activation functions, that neuroscientists either discovered, inspired or exploited to model neurons. Recurrent neural networks are functionally equivalent to systems of partial differential equations and have usefully been described as such in the literature [169, 168, 103, 167, 159]. Finally, neural networks have an advantage over PDE models of aggregate neural function in that they are essentially computational models for manipulating distributed representations in the form of vector-space models by performing relatively simple algebraic transformations that model the behavior of ensembles of relatively simple units.

F — Implementing the model proposed here is challenging for a number of reasons, not the least being the size of the data. Apart from having a lot of computing cycles and fast storage and interconnect hardware, the infrastructure that sits on top of the hardware has to be optimized to handle the particular requirements of large artificial neural networks with billions of parameters. For the most part, Google data centers are designed to handle such workloads. There are some specific patterns of scatter-gather computations that involve working with 3D geometric data that will have to be addressed. The graphic shown in this panel illustrates how network layer (II) responsible for reading in the state vector at time t has to distribute (scatter) information relating to signal propagation, while layer (V) responsible for writing out the state vector at time (t  +  1) has to collect (gather) information relating to signal transmission. The size of these layers is on the order of the number synapses, not neurons.

G — Reconstruction-error adaptive domain selection (READS) is the method whereby we assign each point source corresponding to a recorded neuron in the functional data to a functional (module) basis filter and receptive field. Each functional basis filter has to compete for the privilege to account for each point source. The connections shown in red are trained by gradient descent to apportion point sources on the basis of the corresponding network's ability to predict its output from its input.

References

[1]   Martín Abadi, Ashish Agarwal, Paul Barham, Eugene Brevdo, Zhifeng Chen, Craig Citro, Greg Corrado, Andy Davis, Jeffrey Dean, Matthieu Devin, Sanjay Ghemawat, Ian Goodfellow, Andrew Harp, Geoffrey Irving, Michael Isard, Yangqing Jia, Rafal Jozefowicz, Lukasz Kaiser, Manjunath Kudlur, Josh Levenberg, Dan Mané, Rajat Monga, Sherry Moore, Derek Murray, Chris Olah, Mike Schuster, Jonathon Shlens, Benoit Steiner, Ilya Sutskever, Kunal Talwar, Paul Tucker, Vincent Vanhoucke, Vijay Vasudevan, Fernanda Viégas, Oriol Vinyals, Pete Warden, Martin Wattenberg, Martin Wicke, Yuan Yu, and Xiaoqiang Zheng. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. Tensor Flow Technical Report, 2015.

[2]   Misha B. Ahrens, Jennifer M. Li, Michael B. Orger, Drew N. Robson, Alexander F. Schier, Florian Engert, and Ruben Portugues. Brain-wide neuronal dynamics during motor adaptation in zebrafish. Nature, 485:471--477, 2012.

[3]   Misha B Ahrens, Michael B Orger, Drew N Robson, Jennifer M Li, and Philipp J Keller. Whole-brain functional imaging at cellular resolution using light-sheet microscopy. Nature methods, 10:413--420, 2013.

[4]   Sophie Aimon, Takeo Katsuki, Logan Grosenick, Michael Broxton, Karl Deisseroth, and Ralph J. Greenspan. Activity sources from fast large-scale brain recordings in adult drosophila. bioRxiv, 2015.

[5]   David-Benjamin G. Akalal, Curtis F. Wilson, Lin Zong, Nobuaki K. Tanaka, Kei Ito, and Ronald L. Davis. Roles for drosophila mushroom body neurons in olfactory learning and memory. Learning and Memory, 13:659--668, 2006.

[6]   A. Paul Alivisatos, Miyoung Chun, George M. Church, Ralph J. Greenspan, Michael L. Roukes, , and Rafael Yuste. The brain activity map project and the challenge of functional connectomics. Neuron, 74:970--974, 2012.

[7]   Costas A. Anastassiou, Rodrigo Perin, Henry Markram, and Christof Koch. Ephaptic coupling of cortical neurons. Nature Neuroscience, 14:217--223, 2011.

[8]   Sanjeev Arora, Yuanzhi Li, Yingyu Liang, Tengyu Ma, and Andrej Risteski. Random walks on context spaces: Towards an explanation of the mysteries of semantic word embeddings. CoRR, arXiv:1502.03520, 2015.

[9]   Y. Aso, D. Hattori, Y. Yu, R. M. Johnston, N. A. Iyer, T. T. Ngo, H. Dionne, L. F. Abbott, R. Axel, and G. M. Tanimoto, H. nd Rubin. The neuronal architecture of the mushroom body provides a logic for associative learning. Elife, 3:e04577, 2014.

[10]   Gareth Ball, Paul R. Stokes, Rebecca A. Rhodes, Subrata K. Bose, Iead Rezek, Alle-Meije Wink, Louis-David Lord, Mitul A. Mehta, Paul M. Grasby, and Federico E. Turkheimer. Executive functions and prefrontal cortex: A matter of persistence? Frontiers in Systems Neuroscience, 5:3, 2011.

[11]   Dana H. Ballard. An Introduction to Natural Computation. MIT Press, Cambridge, Massachusetts, 1997.

[12]   C.I. Bargmann. Beyond the connectome: how neuromodulators shape neural circuits. Bioessays, 34:458--465, 2012.

[13]   R.P.J. Barretto and M.J. Schnitzer. In vivo optical microendoscopy for imaging cells lying deep within live tissue. Cold Spring Harbor Protocols, 2012, 2012.

[14]   Sumanta Basu, Ali Shojaie, and George Michailidis. Network granger causality with inherent grouping structure. Journal of Machine Learning Research, 16:417--453, 2015.

[15]   Jason Q. Boone and Chris Q. Doe. Identification of drosophila type II neuroblast lineages containing transit amplifying ganglion mother cells. Devopmental Neurobiology, 68:1185--1195, 2008.

[16]   Antoine Bordes, Xavier Glorot, Jason Weston, and Yoshua Bengio. Joint learning of words and meaning representations for open-text semantic parsing. In Proceedings of the 15th International Conference on Artificial Intelligence and Statistics, 2012.

[17]   Peter Bubenik and Peter T. Kim. A statistical approach to persistent homology, 2006.

[18]   Mark Burgin. Information Theory: a Multifaceted Model of Information. Entropy, 5:146--160, 2003.

[19]   Mark Burgin. Theory of Information: Fundamentality, Diversity and Unification. World Scientific Series in Information Studies. World Scientific Publishing Company, 2010.

[20]   Charles L. Byrne. Alternating minimization as sequential unconstrained minimization: A survey. Journal of Optimization Theory and Applications, 156(3):554--566, 2013.

[21]   Robert A.A. Campbell and Glenn C. Turner. The mushroom body. Current Biology, 20(1):R11--R12, 2010.

[22]   T. Cheatham, A. Fahmy, D. Stefanescu, and L. Valiant. Bulk synchronous parallel computing: A paradigm for transportable software. In Proceedings of the 28th Annual Hawaii Conference on System Sciences, volume II, pages 268--275. IEEE Computer Society Press, 1995.

[23]   Tsai-Wen Chen, Trevor J. Wardill, Yi Sun, Stefan R. Pulver, Sabine L. Renninger, Amy Baohan, Eric R. Schreiter, Rex A. Kerr, Michael B. Orger, Vivek Jayaraman, Loren L. Looger, Karel Svoboda, and Douglas S. Kim. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature, 499:295--300, 2013.

[24]   An-Lun Chin, Chih-Yung Lin, Tsai-Feng Fu, Barry J. Dickson, and Ann-Shyn Chiang. Diversity and wiring variability of visual local neurons in the drosophila medulla m6 stratum. Journal Comparative Neurology, 522:3795--3816, 2014.

[25]   Ya-Hui Chou, Maria L. Spletter, Emre Yaksi, Jonathan C. S. Leong, Rachel I. Wilson, and Liqun Luo. Diversity and wiring variability of olfactory local interneurons in the drosophila antennal lobe. Nature Neuroscience, 13:439--449, 2010.

[26]   Samir Chowdhury and Facundo Mé́moli. Persistent path homology of directed networks. CoRR, arXiv:1701.00565, 2017.

[27]   Louise Couton, Alex S. Mauss, Temur Yunusov, Soeren Diegelmann, Jan Felix Evers, and Matthias Landgraf. Development of connectivity in a motoneuronal network in drosophila larvae. Current Biology, 25:568--576, 2015.

[28]   David Cox. Clique topology reveals intrinsic geometric structure in neural correlations: An overview. CoRR, arXiv:1608.03463, 2016.

[29]   Robbert Creton. Automated analysis of behavior in zebrafish larvae. Behavioural Brain Research, 203(1):127--136, 2009.

[30]   Neil A. Croll. Behavioural analysis of nematode movement. In Ben Dawes, editor, Advances in Parasitology, volume 13, pages 71--122. Academic Press, 1975.

[31]   I. Csiszár and G. Tusnády. Information geometry and alternating minimization procedures. Statistics and Decisions, pages 205--237, 1984.

[32]   C. Curto, S. Sakata, S. Marguet, V. Itskov, and K. D. Harris. A simple model of cortical dynamics explains variability and state dependence of sensory responses in urethane-anesthetized auditory cortex. Journal Neuroscience, 29(34):10600--10612, 2009.

[33]   Carina Curto. What can topology tell us about the neural code?, 2016.

[34]   Carina Curto, Vladimir Itskov, Alan Veliz-Cuba, and Nora Youngs. The neural ring: an algebraic tool for analyzing the intrinsic structure of neural codes. Bulletin of Mathematical Biology, 75(9):1571--1611, 2013.

[35]   Daniel Dennett. From Bacteria to Bach and Back: The Evolution of Minds. W.W. Norton, New York, NY, 2017.

[36]   Peter J. Denning. Ubiquity symposium "What is Computation?": Opening statement. Ubiquity, 2010(November), 2010.

[37]   Pawel Dlotko, Kathryn Hess, Ran Levi, Max Nolte, Michael Reimann, Martina Scolamiero, Katharine Turner, Eilif Muller, and Henry Markram. Topological analysis of the connectome of digital reconstructions of neural microcircuits. CoRR, arXiv:1601.01580, 2016.

[38]   Timothy W. Dunn, Yu Mu, Sujatha Narayan, Owen Randlett, Eva A. Naumann, Chao-Tsung Yang, Alexander F. Schier, Jeremy Freeman, Florian Engert, and Misha B. Ahrens. Brain-wide mapping of neural activity controlling zebrafish exploratory locomotion. eLife, 5:e12741, 2016.

[39]   Herbert Edelsbrunner and John Harer. Persistent homology - a survey. In J. Pach J. E. Goodman and R. Pollack, editors, Surveys on Discrete and Computational Geometry. Twenty Years Later, Contemporary Mathematics, pages 257--282. American Mathematical Society, 2008.

[40]   Benjamin F. Fosque, Yi Sun, Hod Dana, Chao-Tsung Yang, Tomoko Ohyama, Michael R. Tadross, Ronak Patel, Marta Zlatic, Douglas S. Kim, Misha B. Ahrens, Vivek Jayaraman, Loren L. Looger, and Eric R. Schreiter. Labeling of active neural circuits in vivo with designed calcium integrators. Science, 347(6223):755--760, 2015.

[41]   Katerina Fragkiadaki, Pablo Arbelaez, Panna Felsen, and Jitendra Malik. Learning to segment moving objects in videos. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, pages 4083--4090. IEEE Computer Society, 2015.

[42]   J. Friedman, W. Stuetzele, and A. Schroeder. Projection pursuit density estimation. Journal American Statistical Association, 79:599--608, 1984.

[43]   Karl Friston. The free-energy principle: a unified brain theory? Nature Reviews Neuroscience, 11:127--138, 2010.

[44]   Karl Friston and Stefan Kiebel. Predictive coding under the free-energy principle. Philosphical Transactions Royal Society London B Biological Science, 364:1211--1221, 2009.

[45]   Rains G, Kulasiri D, Zhou Z, Samarasinghe S, Tomberlin J, and Olson D. Synthesizing neurophysiology, genetics, behaviour and learning to produce whole-insect programmable sensors to detect volatile chemicals. Biotechnology & Genetic Engineering Reviews, 26:179--204, 2010.

[46]   Mario Galarreta and Shaul Hestrin. Frequency-dependent synaptic depression and the balance of excitation and inhibition in the neocortex. Nature Neuroscience, 1:587--594, 1998.

[47]   Mario Galarreta and Shaul Hestrin. A network of fast-spiking cells in the neocortex connected by electrical synapses. Nature, 402:72--75, 1999.

[48]   Mario Galarreta and Shaul Hestrin. Electrical synapses between gaba-releasing interneurons. Nature Reviews Neuroscience, 2:225--433, 2001.

[49]   Mario Galarreta and Shaul Hestrin. Spike transmission and synchrony detection in networks of gabaergic interneurons. Science, 292:2295--2299, 2001.

[50]   Mario Galarreta and Shaul Hestrin. Electrical and chemical synapses among parvalbumin fast-spiking gabaergic interneurons in adult mouse neocortex. PNAS, 99:12438--12443, 2002.

[51]   Michael Garey and David Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman, New York, NY, 1979.

[52]   Krzysztof J. Geras, Abdel-rahman Mohamed, Rich Caruana, Gregor Urban, Shengjie Wang, Özlem Aslan, Matthai Philipose, Matthew Richardson, and Charles A. Sutton. Compressing LSTMs into CNNs. CoRR, arXiv:1511.06433, 2015.

[53]   Felipe Gerhard, Tilman Kispersky, Gabrielle J. Gutierrez, Eve Marder, Mark Kramer, and Uri Eden. Successful reconstruction of a physiological circuit with known connectivity from spiking activity alone. PLoS Compututational Biology, 9:e1003138, 2013.

[54]   K.K. Ghosh, L.D. Burns, E.D. Cocker, A. Nimmerjahn, Y. Ziv, A.E. Gamal, and M.J. Schnitzer. Miniaturized integration of a fluorescence microscope. Nature Methods, 8:871--8, 2011.

[55]   Matthew R. Gielow and Laszlo Zaborszky. The input-output relationship of the cholinergic basal forebrain. Cell Reports, 18:1817--1830, 2017.

[56]   Chad Giusti, Eva Pastalkova, Carina Curto, and Vladimir Itskov. Clique topology reveals intrinsic geometric structure in neural correlations. Proceedings of the National Academy of Sciences, 112(44):13455--13460, 2015.

[57]   Yiyang Gong, Cheng Huang, Jin Zhong Li, Benjamin F. Grewe, Yanping Zhang, Stephan Eismann, and Mark J. Schnitzer. High-speed recording of neural spikes in awake mice and flies with a fluorescent voltage sensor. Science, 2015.

[58]   C. W. J. Granger. Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37(3):424--438, 1969.

[59]   Alex Graves, Greg Wayne, and Ivo Danihelka. Neural turing machines. CoRR, arXiv:1410.5401, 2014.

[60]   Alex Graves, Greg Wayne, Malcolm Reynolds, Tim Harley, Ivo Danihelka, Agnieszka Grabska-Barwińska, Sergio Gómez Colmenarejo, Edward Grefenstette, Tiago Ramalho, John Agapiou, Adrià Puigdoménech Badia, Karl Moritz Hermann, Yori Zwols, Georg Ostrovski, Adam Cain, Helen King, Christopher Summerfield, Phil Blunsom, Koray Kavukcuoglu, and Demis Hassabis. Hybrid computing using a neural network with dynamic external memory. Nature, 538:471--476, 2016.

[61]   Karol Gregor, Ivo Danihelka, Alex Graves, and Daan Wierstra. DRAW: A recurrent neural network for image generation. CoRR, arXiv:1502.04623, 2015.

[62]   Sten Grillner and Ann M. Graybiel. Microcircuits: The Interface Between Neurons and Global Brain Function. Dahlem Workshop Reports. MIT Press, 2006.

[63]   Sten Grillner, Henry Markram, Erik De Schutter, Gilad Silberberg, and Fiona E. N. LeBeau. Microcircuits in action -- from CPGs to neocortex. Trends in Neurosciences, 28(10):525--533, 2005.

[64]   K. Gurney, T. J. Prescott, and P. Redgrave. A computational model of action selection in the basal ganglia. I. A new functional anatomy. Biological Cybernetics, 84(6):401--410, 2001.

[65]   K. Gurney, T. J. Prescott, and P. Redgrave. A computational model of action selection in the basal ganglia. II. Analysis and simulation of behaviour. Biological Cybernetics, 84:411--423, 2001.

[66]   K. N. Gurney, M. Humphries, R. Wood, T. J. Prescott, and P. Redgrave. Testing computational hypotheses of brain systems function: a case study with the basal ganglia. Network, 15(4):263--290, 2004.

[67]   D. Haber, A. A. C. Thomik, and A. A. Faisal. Unsupervised time series segmentation for high-dimensional body sensor network data streams. In 2014 11th International Conference on Wearable and Implantable Body Sensor Networks, pages 121--126, 2014.

[68]   Richard H. R. Hahnloser, Rahul Sarpeshkar, Misha A. Mahowald, Rodney J. Douglas, and H. Sebastian Seung. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature, 405:947--951, 2000.

[69]   Trevor Hastie, Robert Tibshirani, and Jerome Friedman. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer, New York, 2001.

[70]   Jeff Hawkins and Subutai Ahmad. Why neurons have thousands of synapses, a theory of sequence memory in neocortex. Frontiers in Neural Circuits, 10, 2016.

[71]   M. Heisenberg. Mushroom body memoir: from maps to models. Nature Reviews Neuroscience, 4(4):266--275, 2003.

[72]   Oriol Hinton, Geoff Vinyals and Jeff Dean. Distilling knowledge in a neural network. CoRR, arXiv:1503.02531, 2015.

[73]   Sepp Hochreiter and Jürgen Schmidhuber. Long short-term memory. Neural Computing, 9:1735--1780, 1997.

[74]   Yu Hu, James Trousdale, Kres̈imir Josíc, and Eric Shea-Brown. Motif statistics and spike correlations in neuronal networks. CoRR, arXiv:1206.3537, 2015.

[75]   D. H. Hubel and T. N Wiesel. Integrative action in the cat’s lateral geniculate body. Journal of Physiology, 155:385–398, 1961.

[76]   D. H. Hubel and T. N Wiesel. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. Journal of Physiology, 160:106--154, 1962.

[77]   D. H. Hubel and T. N Wiesel. Receptive fields and functional architecture of monkey striate cortex. Journal of Physiology, 195:215--243, 1968.

[78]   David H. Hubel. Eye, Brain and Vision (Scientific American Library, Number 22). W. H. Freeman and Company, 1995.

[79]   Aapo Hyvarinen. Complexity pursuit: Separating interesting components from time series. Neural Computation, 13:883--898, 2001.

[80]   Elias B. Issa, Charles F. Cadieu, and James J. DiCarlo. Evidence that the ventral stream codes the errors used in hierarchical inference and learning. bioRxiv, 2016.

[81]   K. Ito, K. Shinomiya, M. Ito, J. D. Armstrong, G. Boyan, V. Hartenstein, S. Harzsch, M. Heisenberg, U. Homberg, A. Jenett, H. Keshishian, L. L. Restifo, W. Rossler, J. H. Simpson, N. J. Strausfeld, R. Strauss, and L. B. Vosshall. A systematic nomenclature for the insect brain. Neuron, 81(4):755--765, 2014.

[82]   Michal Januszewski, Jeremy Maitin-Shepard, Peter Li, Jörgen Kornfeld, Winfried Denk, and Viren Jain. Flood-filling networks. CoRR, arXiv:1611.00421, 2016.

[83]   Arnim Jenett, Gerald M. Rubin, Teri-T.B. Ngo, David Shepherd, Christine Murphy, Heather Dionne, Barret D. Pfeiffer, Amanda Cavallaro, Donald Hall, Jennifer Jeter, Nirmala Iyer, Dona Fetter, Joanna H. Hausenfluck, Hanchuan Peng, Eric T. Trautman, Robert R. Svirskas, Eugene W. Myers, Zbigniew R. Iwinski, Yoshinori Aso, Gina M. DePasquale, Adrianne Enos, Phuson Hulamm, Shing Chun Benny Lam, Hsing-Hsi Li, Todd R. Laverty, Fuhui Long, Lei Qu, Sean D. Murphy, Konrad Rokicki, Todd Safford, Kshiti Shaw, Julie H. Simpson, Allison Sowell, Susana Tae, Yang Yu, and Christopher T. Zugates. A GAL4-driver line resource for drosophila neurobiology. Cell Reports, 2:991--1001, 2012.

[84]   P. Jercog, T. Rogerson, and M. J. Schnitzer. Large-scale fluorescence calcium-imaging methods for studies of long-term memory in behaving mammals. Cold Spring Harbor Perspectives in Biology, 8(5), 2016.

[85]   X. Jiang, S. Shen, C. R. Cadwell, P. Berens, F. Sinz, A. S. Ecker, S. Patel, and A. S. Tolias. Principles of connectivity among morphologically defined cell types in adult neocortex. Science, 350(6264):9462, 2015.

[86]   Eric Jonas and Konrad Kording. Could a neuroscientist understand a microprocessor? bioRxiv, 2016.

[87]   Chung M. K., Bubenik P., and Kim P.T. Persistence diagrams of cortical surface data. Information Processing Medical Imaging, 21:386--397, 2009.

[88]   Andrej Karpathy and Fei-Fei Li. Deep visual-semantic alignments for generating image descriptions. In IEEE Conference on Computer Vision and Pattern Recognition, pages 3128--3137, 2015.

[89]   Andrej Karpathy, George Toderici, Sanketh Shetty, Thomas Leung, Rahul Sukthankar, and Li Fei-Fei. Large-scale video classification with convolutional neural networks. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, pages 1725--1732. IEEE Computer Society, 2014.

[90]   Dimitri Kartsaklis, Nal Kalchbrenner, and Mehrnoosh Sadrzadeh. Resolving lexical ambiguity in tensor regression models of meaning. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, pages 212--217, Baltimore, USA, 2014. Association for Computational Linguistics.

[91]   Saul Kato, Harris S. Kaplan, Tina Schrödel, Susanne Skora, Theodore H. Lindsay, Eviatar Yemini, Shawn Lockery, and Manuel Zimmer. Global brain dynamics embed the motor command sequence of caenorhabditis elegans. Cell, 163:656--669, 2015.

[92]   Paul S. Katz and William N. Frost. Intrinsic neuromodulation: altering neuronal circuits from within. Trends in Neurosciences, 19:54--61, 1996.

[93]   Takashi Kawashima, Maarten F. Zwart, Chao-Tsung Yang, Brett D. Mensh, and Misha B. Ahrens. The serotonergic system tracks the outcomes of actions to mediate short-term motor learning. Cell, 2016.

[94]   Jitendra Malik Ke Li. Learning to optimize neural nets. arXiv:arXiv:1703.00441, 2016.

[95]   Diederik P. Kingma and Max Welling. Auto-encoding variational Bayes. CoRR, arXiv:1312.6114, 2013.

[96]   H. Koeppl and S. Haeusler. Motifs, algebraic connectivity and computational performance of two data-based cortical circuit templates. Proceedings of the sixth International Workshop on Computational Systems Biology, pages 83--86, 2009.

[97]   Arun S. Konagurthu and Arthur M. Lesk. On the origin of distribution patterns of motifs in biological networks. BMC Systems Biology, 2:1--8, 2008.

[98]   Mu Li, David G. Andersen, Jun Woo Park, Alexander J. Smola, Amr Ahmed, Vanja Josifovski, James Long, Eugene J. Shekita, and Bor-Yiing Su. Scaling distributed machine learning with the parameter server. In Proceedings of the 11th USENIX Conference on Operating Systems Design and Implementation, pages 583--598, Berkeley, CA, USA, 2014. USENIX Association.

[99]   Yanjie Li, Giorgio Ascoli, Partha P Mitra, and Yusu Wang. Metrics for comparing neuronal tree shapes based on persistent homology. bioRxiv, 2016.

[100]   Ziwei Liu, Xiaoxiao Li, Ping Luo, Chen Change Loy, and Xiaoou Tang. Deep learning markov random field for semantic segmentation. CoRR, arXiv:1606.07230, 2016.

[101]   Aurélie C. Lozano and Vikas Sindhwani. Block variable selection in multivariate regression and high-dimensional causal inference. In Proceedings of the 23rd International Conference on Neural Information Processing Systems, pages 1486--1494. Curran Associates Inc., 2010.

[102]   S. Mallat and Z. Zhang. Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41:3397--3415, 1993.

[103]   Valerio Mante, David Sussillo, Krishna V. Shenoy, and William T. Newsome. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature, 503:78--84, 2013.

[104]   Adam H. Marblestone, Greg Wayne, and Konrad P. Kording. Towards an integration of deep learning and neuroscience. CoRR, arXiv:1606.03813, 2016.

[105]   Gary Marcus, Adam Marblestone, and Thomas Dean. The atoms of neural computation. Science, 346:551--552, 2014.

[106]   Eve Marder. Neuromodulation of neuronal circuits: back to the future. Neuron, 76:1--11, 2012.

[107]   Henry Markram, Eilif Muller, Srikanth Ramaswamy, Michael W. Reimann, Marwan Abdellah, Carlos Aguado Sanchez, Anastasia Ailamaki, Lidia Alonso-Nanclares, Nicolas Antille, Selim Arsever, Guy Antoine Atenekeng Kahou, Thomas K. Berger, Ahmet Bilgili, Nenad Buncic, Athanassia Chalimourda, Giuseppe Chindemi, Jean-Denis Courcol, Fabien Delalondre, Vincent Delattre, Shaul Druckmann, Raphael Dumusc, James Dynes, Stefan Eilemann, Eyal Gal, Michael Emiel Gevaert, Jean-Pierre Ghobril, Albert Gidon, Joe W. Graham, Anirudh Gupta, Valentin Haenel, Etay Hay, Thomas Heinis, Juan B. Hernando, Michael Hines, Lida Kanari, Daniel Keller, John Kenyon, Georges Khazen, Yihwa Kim, James G. King, Zoltan Kisvarday, Pramod Kumbhar, Sebastien Lasserre, Jean-Vincent Le B, Bruno R. C. Magalhes, Angel Merchn-Prez, Julie Meystre, Benjamin Roy Morrice, Jeffrey Muller, Alberto Muoz-Cspedes, Shruti Muralidhar, Keerthan Muthurasa, Daniel Nachbaur, Taylor H. Newton, Max Nolte, Aleksandr Ovcharenko, Juan Palacios, Luis Pastor, Rodrigo Perin, Rajnish Ranjan, Imad Riachi, Jos-Rodrigo Rodrguez, Juan Luis Riquelme, Christian Rssert, Konstantinos Sfyrakis, Ying Shi, Julian C. Shillcock, Gilad Silberberg, Ricardo Silva, Farhan Tauheed, Martin Telefont, Maria Toledo-Rodriguez, Thomas Tränkler, Werner Van Geit, Jafet Villafranca Daz, Richard Walker, Yun Wang, Stefano M. Zaninetta, Javier DeFelipe, Sean L. Hill, Idan Segev, and Felix Schürmann. Reconstruction and simulation of neocortical microcircuitry. Cell, 163:456--492, 2015.

[108]   Nicolas Y. Masse, Sebastian Cachero, Aaron D. Ostrovsky, and Gregory S.X.E. Jefferis. A mutual information approach to automate identification of neuronal clusters in drosophila brain images. Frontiers in Neuroinformatics, 6:21, 2012.

[109]   S. E. McGuire, P. T. Le, and R. L. Davis. The role of Drosophila mushroom body signaling in olfactory memory. Science, 293(5533):1330--1333, 2001.

[110]   Carver Mead. Neural hardware for vision. Engineering & Science, 1:2--7, 1987.

[111]   Carver Mead. Neuromorphic electronic systems. In Proceedings of the IEEE, 1990.

[112]   Tomàs Mikolov, Ilya Sutskever, Kai Chen, Greg Corrado, and Jeffrey Dean. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems 26, pages 3111--3119, 2013.

[113]   Bratislav Misic and Olaf Sporns. From regions to connections and networks: new bridges between brain and behavior. Current Opinion in Neurobiology, 40:1--7, 2016.

[114]   Thomas Mueller. What is the thalamus in zebrafish? Frontiers in Neuroscience, 6, 2012.

[115]   Sarah Feldt Muldoon, Eric W. Bridgeford, and Danielle S. Bassett. Small-world propensity and weighted brain networks. Scientific Reports, 6:22057, 2016.

[116]   Eva A. Naumann, James E. Fitzgerald, Timothy W. Dunn, Jason Rihel, Haim Sompolinsky, and Florian Engert. From whole-brain data to functional circuit models: The zebrafish optomotor response. Cell, 167:947--960, 2016.

[117]   R. K. Naumann, F. Anjum, C. Roth-Alpermann, and M. Brecht. Cytoarchitecture, areas, and neuron numbers of the Etruscan shrew cortex. Journal of Comparative Neurolology, 520(11):2512--2530, 2012.

[118]   Jeffrey P. Nguyen, Ashley N. Linder, George S. Plummer, Joshua, W. Shaevitz, and Andrew M. Leifer. Automatically tracking neurons in a moving and deforming brain. bioRxiv, 2017.

[119]   Jeffrey P. Nguyen, Ashley N. Linder, George S. Plummer, Joshua, W. Shaevitz, and Andrew M. Leifer. Automatically tracking neurons in a moving and deforming brain. IEEE Dataport, 2017.

[120]   Jeffrey P. Nguyen, Frederick B. Shipley, Ashley N. Linder, George S. Plummer, Mochi Liu, Sagar U. Setru, Joshua W. Shaevitz, and Andrew M. Leifer. Whole-brain calcium imaging with cellular resolution in freely behaving caenorhabditis elegans. Proceedings of the National Academy of Sciences, 113:E1074–E1081, 2015.

[121]   C. D. Nichols, J. Becnel, and U. B. Pandey. Methods to assay Drosophila behavior. Journal of Visualized Experience, 61, 2012.

[122]   Maximilian Nickel and Volker Tresp. Tensor factorization for multi-relational learning. In Hendrik Blockeel, Kristian Kersting, Siegfried Nijssen, and Filip Aelezna, editors, Machine Learning and Knowledge Discovery in Databases, volume 8190 of Lecture Notes in Computer Science, pages 617--621. Springer Berlin Heidelberg, 2013.

[123]   Mathias Niepert, Mohamed Ahmed, and Konstantin Kutzkov. Learning convolutional neural networks for graphs. CoRR, arXiv:1605.05273, 2016.

[124]   M. Okun, N. A. Steinmetz, L. Cossell, M. F. Iacaruso, H. Ko, P. Bartho, T. Moore, S. B. Hofer, T. D. Mrsic-Flogel, M. Carandini, and K. D. Harris. Diverse coupling of neurons to populations in sensory cortex. Nature, 521(7553):511--515, 2015.

[125]   Randall C. O'Reilly. Biologically plausible error-driven learning using local activation differences: The generalized recirculation algorithm. Neural Computation, 8(5):895--938, 1996.

[126]   Marius Pachitariu, Carsen Stringer, Sylvia Schröder, Mario Dipoppa, L. Federico Rossi, Matteo Carandini, and Kenneth D. Harris. Suite2p: beyond 10,000 neurons with standard two-photon microscopy. bioRxiv, 2016.

[127]   Karin Panser, Laszlo Tirian, Florian Schulze, Santiago Villalba, Gregory S.X.E. Jefferis, Katja Bühler, and Andrew D. Straw. Automatic segmentation of drosophila neural compartments using GAL4 expression data reveals novel visual pathways. Current Biology, 26:1943--1954, 2016.

[128]   Alessandro E. P. Villa Paolo Masulli. The topology of the directed clique complex as a network invariant. CoRR, arXiv:1510.00660, 2015.

[129]   Josef Parvizi, Gary W. Van Hoesen, Joseph Buckwalter, and Antonio Damasio. Neural connections of the posteromedial cortex in the macaque. Proceedings of the National Academy of Sciences of the United States of America, 103:1563--1568, 2006.

[130]   S. D. Pelkowski, M. Kapoor, H. A. Richendrfer, X. Wang, R. M. Colwill, and R. Creton. A novel high-throughput imaging system for automated analyses of avoidance behavior in zebrafish larvae. Behavioural Brain Research, 223(1):135--144, 2011.

[131]   Rodrigo Perin, Thomas K. Berger, and Henry Markram. A synaptic organizing principle for cortical neuronal groups. Proceedings of the National Academy of Sciences, 108:5419--5424, 2011.

[132]   Simon P. Peron, Jeremy Freeman, Vijay Iyer, Caiying Guo, and Karel Svoboda. A cellular resolution map of barrel cortex activity during tactile behavior. Neuron, 86(3):783--799, 2015.

[133]   Stephen M. Plaza, Toufiq Parag, Gary B. Huang, Donald J. Olbris, Mathew A. Saunders, and Patricia K. Rivlin. Annotating synapses in large EM datasets. CoRR, arXiv:1409.1801, 2014.

[134]   R. Prevedel, Y.G. Yoon, M. Hoffmann, N. Pak, G. Wetzstein, S. Kato, T. Schrödel, R. Raskar, M. Zimmer, E.S. Boyden, and A. Vaziri. Simultaneous whole-animal 3D-imaging of neuronal activity using light field microscopy. CoRR, arXiv:1401.5333, 2013.

[135]   Robert Prevedel, Aart J. Verhoef, Alejandro J. Pernia-Andrade, Siegfried Weisenburger, Ben S. Huang, Tobias Nobauer, Alma Fernandez, Jeroen E. Delcour, Peyman Golshani, Andrius Baltuska, and Alipasha Vaziri. Fast volumetric calcium imaging across multiple cortical layers using sculpted light. Nature Methods, 2016.

[136]   Robert Prevedel, Young-Gyu Yoon, Maximilian Hoffmann, Nikita Pak, Gordon Wetzstein, Saul Kato, Tina Schrodel, Ramesh Raskar, Manuel Zimmer, Edward S. Boyden, and Alipasha Vaziri. Simultaneous whole-animal 3d imaging of neuronal activity using light-field microscopy. Nature Methods, 11:727--730, 2014.

[137]   Owen Randlett, Caroline L. Wee, Eva A. Naumann, Onyeka Nnaemeka, David Schoppik, James E. Fitzgerald, Ruben Portugues, Alix M.B. Lacoste, Clemens Riegler, Florian Engert, and Alexander F. Schier. Whole-brain activity mapping onto a zebrafish brain atlas. Nature Methods, 12:1039--1046, 2015.

[138]   Rajesh P. N. Rao and Dana H. Ballard. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nature Neuroscience, 2:79--87, 1999.

[139]   R. Clay Reid. From functional architecture to functional connectomics. Neuron, 75:209--217, 2012.

[140]   Michael W. Reimann, Costas A. Anastassiou, Rodrigo Perin, Sean L. Hill, Henry Markram, and Christof Koch. A biophysically detailed model of neocortical local field potentials predicts the critical role of active membrane currents. Neuron, 79:375--390, 2013.

[141]   Xiaofeng Ren and Jitendra Malik. Learning a classification model for segmentation. In Proceedings of the Ninth IEEE International Conference on Computer Vision, volume 1, pages 10--17, 2003.

[142]   Paul A. Rhodes and Todd O. Anderson. Evolving a neural olfactorimotor system in virtual and real olfactory environments. Frontiers in Neuroengineering, 5:1--14, 2012.

[143]   Adriana Romero, Nicolas Ballas, Samira Ebrahimi Kahou, Antoine Chassang, Carlo Gatta, and Yoshua Bengio. FitNets: Hints for thin deep nets. CoRR, arXiv:1412.6550, 2014.

[144]   Rahul Sarpeshkar. Analog versus digital: extrapolating from electronics to neurobiology. Neural Computing, 10:1601--1638, 1998.

[145]   Rahul Sarpeshkar. Ultra Low Power Bioelectronics: Fundamentals, Biomedical Applications, and Bio-inspired Systems. Cambridge University Press, 2010.

[146]   K. Sato and K. Touhara. Insect Olfaction: Receptors, Signal Transduction, and Behavior, pages 203--220. Springer Berlin Heidelberg, Berlin, Heidelberg, 2009.

[147]   Benjamin Scellier and Yoshua Bengio. Towards a biologically plausible backprop. CoRR, arXiv:1602.05179v2, 2016.

[148]   Jürgen Schmidhuber. Deep learning in neural networks: An overview. Technical report, Technical Report IDSIA-03-14, 2014.

[149]   Tina Schrödel, Robert Prevedel, Karin Aumayr, Manuel Zimmer, and Alipasha Vaziri. Brain-wide 3D imaging of neuronal activity in caenorhabditis elegans with sculpted light. Nature Methods, 10:1013--1020, 2013.

[150]   H. Sebastian Seung. Neuroscience: Towards functional connectomics. Nature, 471:170--172, 2011.

[151]   C. E. Shannon and W. W. Weaver. The Mathematical Theory of Communication. University of Illinois Press, Urbana, IL, 1949.

[152]   Claude Shannon. A mathematical theory of communication. Bell System Technical Journal, 27:379--423 and 623--656, 1948.

[153]   H. C. Shao, C. C. Wu, G. Y. Chen, H. M. Chang, A. S. Chiang, and Y. C. Chen. Developing a stereotypical drosophila brain atlas. IEEE Transactions on Biomedical Engineering, 61(12):2848--2858, 2014.

[154]   Evan Shelhamer, Jonathan Long, and Trevor Darrell. Fully convolutional networks for semantic segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016.

[155]   Jianbo Shi and Jitendra Malik. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22:888--905, 2000.

[156]   Stewart Shipp, Rick A. Adams, and Karl J. Friston. Reflections on agranular architecture: predictive coding in the motor cortex. Trends in Neurosciences, 36:706--716, 2013.

[157]   Gabriel Silva. Geometric constraints on the dynamics of networks. CoRR, arXiv:1510.08729, 2015.

[158]   Ann Sizemore, Chad Giusti, Richard F. Betzel, and Danielle S. Bassett. Closures and cavities in the human connectome. CoRR, arXiv:1608.03520, 2016.

[159]   Nejib Smaoui and Suad Al-Enezi. Modelling the dynamics of nonlinear partial differential equations using neural networks. Journal of Computational and Applied Mathematics, 170(1):27--32, 2004.

[160]   Richard Socher, John Bauer, Christopher D. Manning, and Andrew Y. Ng. Parsing with compositional vector grammars. In Proceedings of the 51st Annual Meeting of the Association for Computational Linguistics, Stroudsburg, PA, USA, 2013. Association for Computational Linguistics.

[161]   Richard Socher, Alex Perelygin, Jean Y. Wu, Jason Chuang, Christopher D. Manning, Andrew Y. Ng, and Christopher Potts. Recursive deep models for semantic compositionality over a sentiment treebank. In Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing, pages 1631--1642. Association for Computational Linguistics, Stroudsburg, PA, USA, 2013.

[162]   Young Min Song, Yizhu Xie, Viktor Malyarchuk, Jianliang Xiao, Inhwa Jung, Ki-Joong Choi, Zhuangjian Liu, Hyunsung Park, Chaofeng Lu, Rak-Hwan Kim, Rui Li, Kenneth B. Crozier, Yonggang Huang, and John A. Rogers. Digital cameras with designs inspired by the arthropod eye. Nature, 497:95--99, 2013.

[163]   Olaf Sporns and Jonathan D. Zwi. The small world of the cerebral cortex. Neuroinformatics, 2:145--162, 2004.

[164]   M. W. Spratling. A hierarchical predictive coding model of object recognition in natural images. Cognitive Computation, 9(2):151--167, 2017.

[165]   M. Stephenson-Jones, E. Samuelsson, J. Ericsson, B. Robertson, and S. Grillner. Evolutionary conservation of the basal ganglia as a common vertebrate mechanism for action selection. Current Biology, 21(13):1081--1091, 2011.

[166]   James A. Strother, Aljoscha Nern, and Michael B. Reiser. Direct observation of ON and OFF pathways in the drosophila visual system. Current Biology, 24(9):976--983, 2014.

[167]   David Sussillo and L. F. Abbott. Generating coherent patterns of activity from chaotic neural networks. Neuron, 63:544--557, 2009.

[168]   David Sussillo and Omri Barak. Opening the black box: Low-dimensional dynamics in high-dimensional recurrent neural networks. Neural Computation, 25(3):626--649, 2013.

[169]   David Sussillo, Rafal Jozefowicz, L.F. Abbott, and Chethan Pandarinath. LFADS - latent factor analysis via dynamical systems. CoRR, arXiv:1608.06315, 2016.

[170]   Ilya Sutskever, Ruslan Salakhutdinov, and Joshua Tenenbaum. Modelling relational data using bayesian clustered tensor factorization. In Y. Bengio, D. Schuurmans, J. Lafferty, C. K. I. Williams, and A. Culotta, editors, Advances in Neural Information Processing Systems 22, pages 1821--1828. MIT Press, 2009.

[171]   S. Y. Takemura, C. S. Xu, Z. Lu, P. K. Rivlin, T. Parag, D. J. Olbris, S. Plaza, T. Zhao, W. T. Katz, L. Umayam, C. Weaver, H. F. Hess, J. A. Horne, J. Nunez-Iglesias, R. Aniceto, L. A. Chang, S. Lauchie, A. Nasca, O. Ogundeyi, C. Sigmund, S. Takemura, J. Tran, C. Langille, K. Le Lacheur, S. McLin, A. Shinomiya, D. B. Chklovskii, I. A. Meinertzhagen, and L. K. Scheffer. Synaptic circuits and their variations within different columns in the visual system of Drosophila. Proceedings of the National Academy of Science, 112(44):13711--13716, 2015.

[172]   Shin-ya Takemura, Arjun Bharioke, Zhiyuan Lu, Aljoscha Nern, Shiv Vitaladevuni, Patricia K. Rivlin, William T. Katz, Donald J. Olbris, Stephen M. Plaza, Philip Winston, Ting Zhao, Jane Anne Horne, Richard D. Fetter, Satoko Takemura, Katerina Blazek, Lei-Ann Chang, Omotara Ogundeyi, Mathew A. Saunders, Victor Shapiro, Christopher Sigmund, Gerald M. Rubin, Louis K. Scheffer, Ian A. Meinertzhagen, and Dmitri B. Chklovskii. A visual motion detection circuit suggested by drosophila connectomics. Nature, 500:175--181, 2013.

[173]   C. M. Thibeault and N. Srinivasa. Using a hybrid neuron in physiologically inspired models of the basal ganglia. Frontier Computational Neuroscience, 7:88, 2013.

[174]   Robert Tibshirani. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 58(1):267--288, 1996.

[175]   Naftali Tishby and Noga Zaslavsky. Deep learning and the information bottleneck principle. CoRR, arXiv:1503.02406, 2015.

[176]   Gašper Tkački, Olivier Marre, Dario Amodei, Elad Schneidman, William Bialek, and Michael J. Berry, II. Searching for collective behavior in a large network of sensory neurons. PLOS Computational Biology, 10:1--23, 2014.

[177]   Daniel B. Turner-Evans and Vivek Jayaraman. The insect central complex. Current Biology, 26(11):R453--R457, 2016.

[178]   Gregor Urban, Krzysztof J. Geras, Samira Ebrahimi Kahou, Özlem Aslan, Shengjie Wang, Rich Caruana, Abdelrahman Mohamed, Matthai Philipose, and Matthew Richardson. Do deep convolutional nets really need to be deep (or even convolutional)? CoRR, arXiv:1603.05691, 2016.

[179]   Eleni Vasilaki and Michele Giugliano. Emergence of connectivity motifs in networks of model neurons with short- and long-term plastic synapses. CoRR, arXiv:1301.7187, 2013.

[180]   James E. Vaughn, Terry Sims, and Mariko Nakashima. A comparison of the early development of axodendritic and axosomatic synapses upon embryonic mouse spinal motor neurons. The Journal of Comparative Neurology, 175:79--100, 1977.

[181]   John von Neumann. Probabilistic logics and the synthesis of reliable organisms from unreliable components. In Claude E. Shannon and John McCarthy, editors, Automata Studies, pages 329--378. Princeton University Press, Princeton, NJ, 1956.

[182]   Y. Weiss. Segmentation using eigenvectors: a unifying view. In Proceedings of the Seventh IEEE International Conference on Computer Vision, volume 2, pages 975--982, 1999.

[183]   Tanya Wolff, Nirmala A. Iyer, and Gerald M. Rubin. Neuroarchitecture and neuroanatomy of the drosophila central complex: A GAL4-based dissection of protocerebral bridge neurons and circuits. Journal Comparative Neurology, 523:997--1037, 2015.

[184]   X. Xie and H. S. Seung. Equivalence of backpropagation and contrastive Hebbian learning in a layered network. Neural Computation, 15(2):441--454, 2003.

[185]   C. Xu, C. Lu, X. Liang, J. Gao, W. Zheng, T. Wang, and S. Yan. Multi-loss regularized deep neural network. IEEE Transactions on Circuits and Systems for Video Technology, 26(12):2273--2283, 2016.

[186]   Yongxin Yang and Timothy M. Hospedales. Deep multi-task representation learning: A tensor factorisation approach. CoRR, arXiv:605.06391, 2016.

[187]   Raphael Yuste. From the neuron doctrine to neural networks. Nature Reviews Neuroscience, 16(8):487--497, 2015.

[188]   Barret Zoph and Quoc V. Le. Neural architecture search with reinforcement learning. In Proceedings of the 5th International Conference on Learning Representations, 2017.

1 Specifically, Stephen writes: "I would think the location of the arbors should allow proper registration with confocal data / functional data. It is my understanding that soma location can vary from sample to sample a little bit—in the fly, as you know, the soma are usually smashed on the edge of the tissue and the main interior regions where the connections occur are dominated by dense non-soma neuropil. I would expect arbor location to be very stereotyped.

2 In the online [4] supplementary materials, the authors note that: "Currently, the registration of the maps with the anatomy is done using landmark registration. This method is imprecise in brain areas that lack clear landmarks. Concurrently imaging the brains using a different microscopy technique with higher resolution could help detect more landmarks or make it possible to use different registration techniques. Automatizing the search for matches between the maps and neurons in large databases such as flycircuit or virtual fly brain would help to get to the level of neurons rather than brain regions".

3 Here is a suggestion for using visual test-patterns as stimuli during functional recording to facilitate aligning functional and structural data involving topographically mapped areas of the visual system, such as retinotopic maps in the case of mammals:

Figure 4:  This graphic illustrates how a test stimuli might be used to help in aligning functional and structural data in the case in which we know something about the structure and function of some portion of the target tissue sample. In this case, suppose the sample is from drosophila and includes some portion of the medulla in the fly visual system covering a number of columns shown here as hexagons. The stimulus depicted in the graphic consists of a shadow moving across the visual field. We should expect to see autocorrelated features corresponding to a wave of activity in the columns with a period proportional to the rate at which the shadow is moving. We might use multiple trials in which the shadow moves in different directions to resolve ambiguity in the estimated correspondences or a less symmetrical stimulus in the same way one uses structured light to estimate the pose of the objects in a scene.

4 Art Pope wrote that, "[p]erhaps your goal is to identify the voxels of the calcium image sequence that are part of the medulla (or some other region of interest). If so, there may be easier ways to accomplish that. Less difficult than recovering whole surfaces in the calcium image data would be locating a few fiducials, even manually, and associating those fiducials with atlas locations. Or perhaps a fly could be imaged with marker beads positioned at known locations. In either case, three points would define a rigid transform between the two volumes; more points would reduce uncertainty and/or resolve deformation."

5 Earlier note with simplified description and additional notes:

  1. From: Data and tools from Janelia FlyLight [83] team and their collaborations → 3D mesh model of adult fly brain;
    Note: VirtualFlyBrain github repositories appear to include 3D mesh models of all major neuropil including the medulla;

  2. From: Sophie Aimon & team @ Greenspan's lab: → 3-D point cloud of pre-processed CI data neuron coordinates;
    Note: High resolution full (half) brain CI datasets will require combining four (two) smaller ~ 300 ×150 ×150 μm datasets;

  3. Fit 3D mesh model to 3D point cloud using standard tools or use one of the existing anatomical reference toolkits:
    Note: The 3D mesh model is not convex hull, but includes surfaces of all fissures and so has accurate sub volume fiducials;

  4. Using the coordinates of the 3D mesh of the medulla subvolume, extract medulla point clouds from each 3D frame;

  5. Construct the 3D point cloud corresponding to the coordinates of all cell bodies included in the seven-column data;

  6. Find the best match or matches that map excitations registered in the CI data with seven-column soma coordinates;

6 Compared with confocal and two-photon fluorescence microscopy, light-sheet exposes the embryo to at least three orders of magnitude less light energy, but still provides up to 50 times faster imaging speeds and a 10–100-fold higher signal-to-noise ratio.

7 "[W]e introduce a set of practical methods based on novel clustering algorithms, and provide a complete pipeline from raw image data to neuronal calcium traces to inferred spike times. We formulate a generative model of the fluorescence image, incorporating spike times and a spatially smooth neuropil signal, and solve the inference and learning problems using a fast algorithm. This implementation scales linearly with the number of recorded cells, and [...] runs in approximately one hour for typical two-hour long recordings, on commodity GPUs." From the abstract of [126].

8 Here is the format specification for Marius Pachitariu's mouse cortex data. The data is fully processed, so there is no need to use Suite2p to perform any additional processing, just load it into Matlab. The data also includes the pupil area of the mouse, which, at the time the experiments were conducted, was the only behavioral measure monitored. Otherwise, this is purely spontaneous activity in the dark, but it has a lot of structure that would be interesting to analyze—see this movie: 

Ff = number of timepoints by number of cells, raw fluorescence trace
dcell = number of cells by 1. 
dcell{n}.st = spike/burst times
dcell{n}.c  = magnitude of the burst

In principle, you can also get the pupil area from infExp1.pupil.area, but you will have to interpolate this to the number of frames in the raw data. The pupil recording and the spiking recording are aligned—that is they were started and stopped at exactly the same time.

9 The Virtual 6502 is probably your best bet, but there are also game console emulators like Stella and a bunch of emulators for the chip that powers the console.

10 And ultimately led me by a circuitous path to discover John Conway and then to Donald Knuth’s wonderful book: Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness.

11 Mathematically, the micro-, meso- and macro-scale models correspond to separate but related dynamical systems, each model employing a different representation of phase space. The mapping from meso-scale phase space to micro-scale phase space is onto but not one-to-one, i.e., it is surjective but not injective and hence not invertible.

12 Building a model detailed enough to simulate pathological behavior is challenging to say the least. Even if we understood the underlying biology in sufficient detail to construct an accurate model, covering the full panoply of pathologies from the microscale, e.g., genetic mutations from exposure to toxic chemicals, to the macro, e.g., inflammation due to cerebral contusions, it is very likely to be intractable for all but the simplest organisms, most certainly ill posed given the many ways that a given symptom or superficial observation may present itself.

13 The word ensemble is commonly used to refer to a group of musicians, actors or dancers who perform together, or, more generally, to a group of items viewed as a whole rather than individually. In the present context, the latter is preferred when discussing ensembles of neurons, not simply to resist anthropomorphizing neurons, but to avoid imputing any sense of agency or organized activity except at the aggregate level. This sense of the word is more in keeping with the concept of a statistical ensemble and its application in themodynamics and the kinectic theory of gases.

14 Retinotopy is the mapping of visual input from the retina to neurons, particularly those neurons within the visual stream. For clarity, 'retinotopy' can be replaced with 'retinal mapping', and 'retinotopic' with 'retinally mapped'. (SOURCE)

15 Somatotopy is the point-for-point correspondence of an area of the body to a specific point on the central nervous system. Typically, the area of the body corresponds to a point on the primary somatosensory cortex (postcentral gyrus). The motor and sensory cortices of the brain are arranged somatotopically, specific regions of the cortex being responsible for different areas of the body. (SOURCE)

16 The hippocampus and entorhinal cortex have specialized types of pyramidal neurons called place cells and grid cells that assist in navigation and orientation by encoding the speed and direction of movement as well as information about specific locations including their position and distance relative to the organism.

17 One can descend further using flip-flops, logic gates, multiplexers, processor clocks, serial interfaces, transistors and further still using the language of semiconductor physics involving conduction-bands, depletion zones, band-gap energy and quantum tunneling, but this level of detail is generally not required by programmers in order for them to write good code. This is because solid-state physicists and electrical engineers have been able to develop devices that exhibit extraordinarily stable behavior over broad range operating conditions. We can't expect this sort of stability and well-defined conceptual boundaries in biological systems and will inevitable have to satisfy ourselves with somewhat porous abstractions.

18 In neuroanatomy, a nucleus (plural form: nuclei) is a cluster of densely packed cell bodies of neurons in the central nervous system, located deep within the cerebral hemispheres and brainstem. The neurons in one nucleus usually have roughly similar connections and functions. Nuclei are connected to other nuclei by tracts, the bundles (fascicles) of axons (nerve fibers) extending from the cell bodies. A nucleus is one of the two most common forms of nerve cell organization, the other being layered structures such as the cerebral cortex or cerebellar cortex. In anatomical sections, a nucleus shows up as a region of gray matter, often bordered by white matter. The vertebrate brain contains hundreds of distinguishable nuclei, varying widely in shape and size. A nucleus may itself have a complex internal structure, with multiple types of neurons arranged in clumps (subnuclei) or layers. (SOURCE)

19 The single-instruction-multiple-data (SIMD) devices familiar to the current generation of programmers in the form of graphics processing units (GPU) can approximate PRAM algorithms. Jeff Dean and Ghemawat's MapReduce model and Valiant's [22] bulk synchronous parallel (BSP) model, are multiple-instruction, multiple-data (MIMD) models and are often referred to as bridging models that assist programmers in designing parallel algorithms.

20 We can model the sort of complex problem solving and decision making generally attributed to the anterior frontal cortex—commonly referred to as the prefrontal cortex—using a class of neural networks that can read from and write to an external, content-addressable memory and be trained with reinforcement learning[60]. Reading and writing is accomplished by attentional networks that focus on locations in memory containing content similar to an address vector, enable sequential reads and allocate locations in memory for writes that, like their biological counterpart, can result in changes to nearby locations in memory [61, 59]. These extended neural networks, called differentiable neural computers, are able to solve problems that require remembering items indefinitely, as in the case of manipulating complex objects like social networks, circuit diagrams or geographical maps. The ability to retain information in memory using temporally persistent neural activity appears to be critical in supporting this sort of reasoning [10].

21 In recent years, engineers have come to appreciate and exploit the benefits of artificial neural networks. In particular biological and artificial networks have provided new insights into solving seemingly intractable optimization and scheduling problems. These problems have been shown to belong to hard complexity classes. Neural networks avoid contradicting the existing theoretical results by not solving the general form of these problems, instead using a combination of memorization and pattern recognition to generate approximate solutions for frequently occurring instances. Instead of solving instances of the (intractable) vehicle-routing or the (intractable) bin-packing problem [51], we solve instances of the (specific) UPS-delivery-truck-routing-for-greater-Seattle problem or the Walmart-multiple-purchase-single-destination-shipping-container-packing problem thereby exploiting the following observations: Not all instances of the routing and packing problems are worth spending the effort to solve optimally. Some parts of the city have few deliveries while others routinely have many. Shipping containers come in fixed sizes and most individual-product packaging is standardized.

It is prohibitively expensive to memorize solutions to all instances, but artificial neural networks can find good solutions to the most common problem instances. Moreover, you don't have to be clever to generate such solutions; you simply have to collect enough of the right sort of data so important special cases and relevant patterns stand out. It is surprising how many problems yield to this approach, including a wide range of combinatorial optimization problems [169, 175, 95]. This approach to solving optimization problems hasn't received much attention until recently, in part because the dominant model of algorithmic thinking is based on an architecture very different from that inherent in biological computing.

22 Olaf Sporns at Indiana University and Patric Hagmann at Lausanne University Hospital independently and simultaneously suggested the term connectome to refer to a map of the neural connections within the brain. This term was directly inspired by the ongoing effort to sequence the human genetic code—to build a genome. (SOURCE)

23 Often hundreds to thousands of axodendritic and axosomatic synapses will occur on a single motor neuron. There is some evidence to suggest that early-forming axosomatic synapses may facilitate dendritic development once it has been induced: "This possibility is discussed in terms of our observation that early-forming axosomatic synapses rather commonly occur at sites which may represent somal growth regions. This relationship leads us to suggest that early axosomatic synapses may facilitate dendritic development by signaling the motor somata that the formation of a synaptogenic axonal field is underway. Furthermore, we speculate that the positioning of early axosomatic contacts might be providing directive cues as to the location of the developing synaptogenic field. Thus a directive facilitation of dendritic growth is suggested as a function of early axosomatic synapses rather than one involved with the primary induction of dendrogenesis." [180]

24 An algorithm is a step-by-step procedure for solving a computational problem. A computational problem might have several algorithms with different average-, best- and worst-case performance. Sorting a list of n items is a good example: quicksort and insertion sort are worst-case O( n2 ), while mergesort and heapsort are both O( n log(n) ). The expression O(…) is big-O notation and is used to express the limiting behavior—up to a constant factor in the present example—of an algorithm in applying asymptotic analysis to classify algorithms by how they respond to changes in input size. An algorithm can have several implementations, employing different programming languages, different coding styles and having different hardware requirements.

25 In attempting to simplify the terminology I use in giving talks about mesoscale modeling and tailor the delivery to different audiences as well as mixed audiences, I looked in the literature for consensus about the meaning of the terms used by computational neuroscientists and computer scientists working on computer-vision and image-processing problems to talk about convolutions. Here are the best sources I found for the use of the terms receptive field and filter kernel:

When dealing with high-dimensional inputs such as images, as we saw above it is impractical to connect neurons to all neurons in the previous volume. Instead, we will connect each neuron to only a local region of the input volume. The spatial extent of this connectivity is a hyperparameter called the receptive field of the neuron (equivalently this is the filter size). (SOURCE)

In addition to the definition below, the term filter kernel is often used as a synonym for kernel function when speaking about the obvious generalization of convolution. Different disciplines talk about filters as predicates on structured lists, tables or tensors. The term is also used in machine learning, especially with regard to support vector machines that are also referred to as kernel machines. In many but not all cases, the kernel function is the dot product of the convolution matrix and a filter-sized region of the target data, i.e., matrix, volume or other structured data.

In image processing, a kernel, convolution matrix, or mask is a small matrix. It is useful for blurring, sharpening, embossing, edge detection, and more. This is accomplished by means of convolution between a kernel and an image. (SOURCE)

In functional programming, a filter is a higher-order function that processes a data structure (usually a list) in some order to produce a new data structure containing exactly those elements of the original data structure for which a given predicate returns the Boolean value true. (SOURCE)

26 From an information-processing perspective the recording sites can be thought of as unidirectional streams of data. While it is interesting to contemplate how one might implement some form of retrograde signaling in this model, we defer that discussion to another time.

27 More precisely, if the functional domains are pairwise disjoint, they constitute a partition also called an exact cover. If at least one pair of domains has a nonempty intersection, they constitute non-exact cover. It seems unlikely that set of functional domains will be pairwise disjoint. Biology is seldom so neat and tidy, especially in the case of neural computation where neural circuits often appear to play supporting roles serving multiple functions.

28 An alternative interpretation of dF is as the change Δ in fluorescence F relative to some baseline F0 which is used as a proxy for changes in the concentration of Ca+2. For example, Nguyen et al [120] represent the signal from a given neuron as "the fractional change from baseline of the ratios of the green- and red-channel fluorescence intensity, ΔR = R0 after accounting for photobleaching", and Kato et al [91] comment that the "single-cell fluorescence intensity F was computed by taking the average of the brightest 75 voxels at every time point after subtracting a z-plane specific background fluorescence intensity. ΔF/F0 was computed for each neuron with F0 taken as the mean fluorescence intensity across the trial."

29 The domain of a function f : X → Y is the set X of possible values of the independent variable x. The range of f is the set Y of resulting values f (x) of the dependent variable y.

30 The term "interface" also alludes to the notion of an application programming interface (API). An API describes how software components should interact. In object oriented programming, a good API hides implementation details, revealing only what a programmer needs to know to use the advertised functionality. In neural circuits, the separation between a function and its implementation is more porous.

31 The retrieval strategy described here is related to scatter-gather memory indexing, which is a "method of addressing vectors in sparse linear algebra operations that is the vector-equivalent of register indirect addressing, with gather involving indexed reads and scatter indexed writes." (SOURCE)

32 In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. Any cut determines a cut-set, the set of edges that have one endpoint in each subset of the partition. These edges are said to cross the cut. (SOURCE)

33 "In fact, individual neurons can participate in different functional groups, flexibly reorganizing themselves and diluting the concept of the receptive field. This combinatorial flexibility, originally proposed by Hebb, is a natural consequence of synaptic plasticity and it also allows the modular composition of small assemblies into larger ones. Because of this flexibility, neural circuits may never be able to be in the same functional state twice, responding differently even if the exact same sensory stimulus is presented." Raphael Yuste [187].

34 Okun et al [124] provide evidence supporting their hypotheses that "population coupling provides a compact summary of population activity; knowledge of the population couplings of n neurons predicts a substantial portion of their n2 pairwise correlations. Population coupling therefore represents a novel, simple measure that characterizes the relationship of each neuron to a larger population, explaining seemingly complex network firing patterns in terms of basic circuit variables." Tkački et al [176] show that "neural ensembles are extremely inhomogenous" and demonstrate convincingly that "the state of individual neurons is highly predictable from the rest of the population, allowing the capacity for error correction"

35 The basic idea of building reliable circuits from unreliable components has been around since the dawn of modern computing [181]. John von Neumann, Claude Shannon and Carver Meade were among its early advocates, but semiconductor manufacturers managed to provide such reliability in the performance of individual VLSI components, and transistor logic gates in particular, that interest in applying the principle waned in the latter part of the 20th century. Only recently has it become appreciated that the price of such reliability at the submicron scale is power, and interest in building circuits that operate in the subthreshold regime has seen a revival [144, 145]. Carver Meade is said to have opined that individual neurons have little value as first-rate circuit elements and that advocates of low-power neuromorphic computing [111, 110] should take a hint from nature in engineering fault tolerance into circuits by replicating and integrating the behavior of simple, efficient but unreliable components.

36 Capacitative leakage current during device idle mode is the main factor responsible for static power dissipation in computer processor chips. Such leakage currents have been increasing dramatically as components and interconnect processes dip below 100 nm. They have thwarted industry attempts to build low-power devices and make it more difficult to implement reliable nontraditional computing elements that employ transistors operating in the subthreshold regime [145, 68, 144]. Of course, such currents are not signaling pathways per se but rather nuisance factors that we seek to minimize or eliminate altogether. In the brain, diffuse signaling pathways play an important computational role in a wide range of behavioral circumstances. Neuromodulation is one such pathway [106, 53, 12, 92, 92]. Ephaptic coupling, in which fluctuating extracellular fields feed back onto the electric potential across the neuronal membrane independent of the activity of synapses, is yet another [7].

37 Amy Christensen and Saurabh Vyas' project in CS379C initially focused on using Granger causality to analyze data generated by Costas Anastassiou's large-scale cortex simulation. They eventually gave up on Granger causality and ended up fitting a dynamical system with a point process wrapped in a hidden Markov model framework. The model parameters were estimated using expectation maximization.

38 This alternative version of Figure 22 [...]

Figure 23:  [...] this factored verson of the point source module assignment layer illustrated in Figure 22 allows [...]

39 The anchor in the main text corresponding to this footnote shows an early version of the model below which was first presented at Lawrence Berkeley National Laboratories on February 8, 2017. In some respects I prefer this sketch as it natually builds graphically and conceptually on Figure 13. A cleaned up version of this graphic combined with Figure 13 and Figure 21 might work better for shorter presentations such as the Keystone Symposium:

Figure 26:  This figure builds on Figure 13 by providing detail on how the sparse functional basis is trained. In the following, the Ai assign point sources (cells) to functional domains, the Bi indicate basis filters and their corresponding functional networks, the Ci constitute local cost / loss functions, the Di corresponding to forward-propagating mux (multiplexer) / backward-propagating demux (demultiplexers) units, and E is the global loss comparing predicted and observed output. Three basis filters {f1, f2, f3} and their associated functional modules {B1, B2, B3} are shown. The graphic illustrates the application of these three filters to the spherical subvolume corresponding to the receptive-field centered at location μi.

The functional interfaces for the three filters are shown using the same graphical conventions introduced in Figure 21, specifically, the network components {A1, A2, A3} that assign point sources to functional domains and the origin of their parameters in the filter-location specific regions of the configuration layer. Note that in this example all three of the interface components Ai receive input from the same point sources. The graphic focuses on how the basis filters are evaluated at location μi, how values obtained from different filters at the same location compete with one another to account for the module-level predictions at that location, and how values obtained from two different locations μi and μj are combined to generate predictions for entire model. Not shown are the sparsity-inducing components that ensure each point source / cell is assigned to exactly one functional module domain.

To reiterate and emphasize key points from earlier figures, each filter has a set of location-filter-specific parameters that encode a local impedance-matching embedding and serve to determine its functional domain at each location by restricting the set of point sources / vertices that constrain the local maximally enclosed subgraph of the connectome graph, i.e., the spherical subvolume that constitutes the receptive field centered at 3D grid location μi in the microcircuit-connectome-graph embedding. The configuration layer sub-region labeled f* assigns a filter-location-specific scalar value (weight) in the unit interval to each basis filter thereby determining a linear combination of the basis filters at each location. Two loss functions are shown: a local loss that minimizes the reconstruction error of each functional module in predicting its outputs from its inputs and a global loss that accounts for all of the outgoing / efferent / behavioral output. Not shown is the sparsity-inducing term in the global loss that ensures for any given location that the weights of the corresponding linear combination of basis filters are mostly zero.

40 Here are some numbers for potential model mammals — and one avian — having relatively small brains and exhibiting behaviors rich enough to be of interest to neuroscientists:

  1. Etruscan shrew ~10,000,000 neurons in just the cortex [117] (SOURCE) @ ~1.8g — The Etruscan shrew (Suncus etruscus), also known as the Etruscan pygmy shrew or the white-toothed pygmy shrew is the smallest known mammal by mass, weighing only about 1.8 grams (0.063 oz) on average—the bumblebee bat is regarded as the smallest mammal by skull size. The Etruscan shrew has a body length of about 4 centimetres (1.6 in) excluding the tail. It is characterized by very rapid movements and a fast metabolism, eating about 1.5–2 times its own body weight per day. (SOURCE)

  2. Smoky shrew ~36,000,000 neurons (SOURCE) @ ~5g — The smoky shrew (Sorex fumeus) is a medium-sized North American shrew found in eastern Canada and the northeastern United States and extends further south along the Appalachian Mountains. The smoky shrew is active year-round. It is dull grey in colour with lighter underparts and a long tail which is brown on top and yellowish underneath. During winter, its fur is grey. Its body is about 11 centimetres (4.3 in) in length including a 4 centimetres (1.6 in) long tail and it weighs about 5 grams (0.18 oz). (SOURCE)

  3. Short-tailed shrew ~52,000,000 neurons (SOURCE) @ ~14g — The Southern short-tailed shrew is the smallest shrew in the genus Blarina, a group of relatively large shrews with relatively short tails found in North America. It measures 7 to 10 cm (2.8 to 3.9 in) in total length, and weighing less than 14 g (0.49 oz). It has a comparatively heavy body, with short limbs and a thick neck, a long, pointed snout and ears that are nearly concealed by its soft, dense fur. As its name indicates, the hairy tail is relatively short, measuring 1.2 to 2.5 cm (0.47 to 0.98 in). The feet are adapted for digging, with five toes ending in sharp, curved claws. The fur is slate gray, being paler on the underparts. (SOURCE)

  4. House mouse ~71,000,000 neurons and ~1012 (one thousand billion or one trillion) synapses (SOURCE) @ ~40-45g — The house mouse (Mus musculus) is a small mammal of the order Rodentia. The adult has a body length (nose to base of tail) of 7.5–10 cm (3.0–3.9 in) and a tail length of 5–10 cm (2.0–3.9 in). The weight is typically 40–45 g (1.4–1.6 oz). Laboratory mice derived from the house mouse are by far the most common mammalian species used in genetically engineered models for scientific research. (SOURCE)

  5. Zebra finch ~131,000,000 not including any perpheral nerves, just the brain (SOURCE) @ 15g — Zebra finch males learn their songs from their surroundings, and are often used as avian model organisms to investigate the neural bases of learning, memory, and sensorimotor integration. They average 4 inches (10 cm) in length, weigh between 10 and 30 grams—published estimates vary, and live on average 4 to 9 years—compared with Drosophila melanogaster 28 days, C. elegans 2-3 weeks, Etruscan shrew 2 years and Danio rerio 42 months. (SOURCE)

41 In simplifying the terminology used to describe mesoscale modeling, we searched the literature for agreement on the meaning of the terms used by computational neuroscientists and computer scientists working on computer and natural vision to talk about filters, convolutions, etc. There was no consensus as far as we could tell, but here are the best sources we found for the use of the terms receptive field and filter kernel:

When dealing with high-dimensional inputs such as images, as we saw above it is impractical to connect neurons to all neurons in the previous volume. Instead, we will connect each neuron to only a local region of the input volume. The spatial extent of this connectivity is a hyperparameter called the receptive field of the neuron (equivalently this is the filter size). (SOURCE)

In addition to the definition below, the term filter kernel is often used as a synonym for kernel function when speaking about the obvious generalization of convolution. Different disciplines talk about filters as predicates on structured lists, tables or tensors. The term is also used in machine learning, especially with regard to support vector machines that are also referred to as kernel machines. In many but not all cases, the kernel function is the dot product of the convolution matrix and a filter-sized region of the target data, i.e., matrix, volume or other structured data.

In image processing, a kernel, convolution matrix, or mask is a small matrix. It is useful for blurring, sharpening, embossing, edge detection, and more. This is accomplished by means of convolution between a kernel and an image. (SOURCE)

In functional programming, a filter is a higher-order function that processes a data structure (usually a list) in some order to produce a new data structure containing exactly those elements of the original data structure for which a given predicate returns the Boolean value true. (SOURCE)

In the fields of neuroscience and neurobiology, the term is used rather broadly and often inconsistently, but the general idea is that the receptive field of a cell in primary sensory and motor cortex constitutes a set of receptors often arranged in a contiguous region in one of the many topographic maps that organize our sensorimotor experience in accord with the relevant geometry of our bodies and physical environment. The following excerpt from David Hubel's primer on vision [78] provides a good introduction:

Narrowly defined, the term receptive field refers simply to the specific receptors that feed into a given cell in the nervous system, with one or more synapses intervening. In this narrower sense, and for vision, it thus refers simply to a region on the retina, but since Kuffler's time and because of his work the term has gradually come to be used in a far broader way. (SOURCE)