Final Project Proposals

Analyzing Connectomic Networks

The landing page for the Network Data Analysis group at Ohio State University can be found here. If you want to get up to speed on their approach as outlined in Chowdhury and Memoli [7], Peter Li suggested the following progression: one, two, three and four. The first three just develop and apply the Dowker Complex as a simplicial complex sensitive to asymmetry, but without a homological operator that retains asymmetries, so the sensitivity of the overall persistence diagrams to asymmetry is modest.

The last paper—four—makes the additional step of introducing ordered simplices and ordered homology, so the resulting persistence strongly reflects asymmetries. Pawel Dlotko notes that this is computationally expensive, and Peter Li¹ has concerns about its practicality and is not sure how good the available software support is. If you are already familiar with persistence over simplicial complexes from presentation by Pawel Dlotko² last year (VIDEO), you can probably jump right into the last paper, but you may find it helpful to go through all of them just to get multiple restatements of the same information as well as to understand the progression. Both Peter and Pawel would be happy to help out teams working on this topic.

Sebastian Seung's Presentation

Papers on Seung and Zung's Correlation Game plus two of Peter Földiák's papers: [Seung and Zung], [Carlson], [Földiák], [Földiák]

Drosophila Structure and Function

Papers on Drosophila Structure and Function — click on the item for the PDF: Neriec and Desplan, Plaza et al, Takemura et al, Borst and Euler, Spalthoff, Joesch et al, Erclik et al, Mauss et al, Borst, Bahl et al, Maisak et al, Reiff et al, Borst and Helmstaedter, Behnia et al, Morante and Desplan. Art Pope³ would be happy to help out teams working on applying graph search and computer vision algorithms to the Janelia data.

the Here are a few visual aids selected from the these papers:

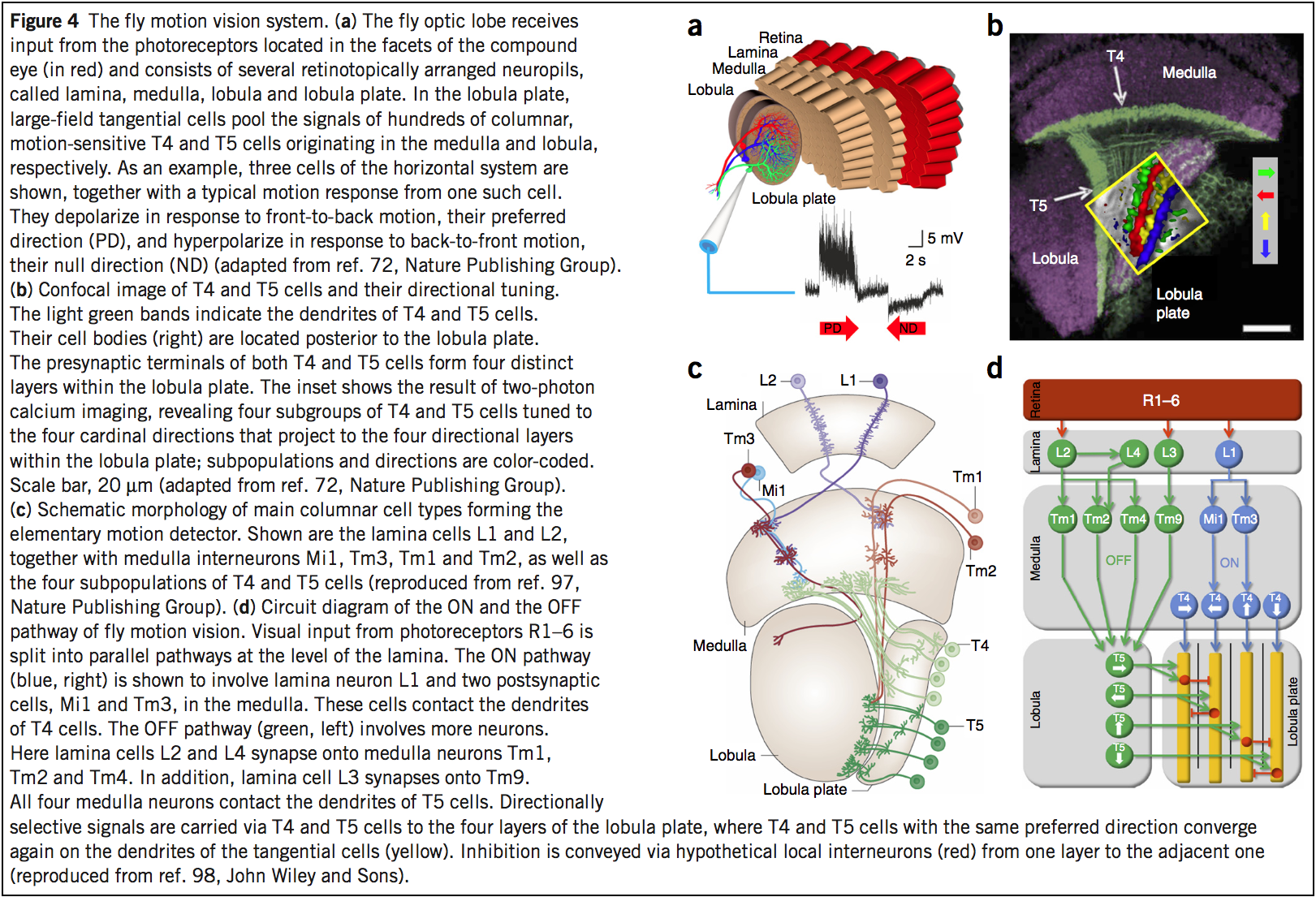
Borst and Helmstaedter [5] Figure 4:

Behnia et al [2] Figure 1:

Morante and Desplan [15] Figure 2:

Seven Column Medulla Dataset

The Python code for exploring the seven-column dataset and analyzing the data using ideas from algebraic topology can be found here: [NEUROBOT] [CODE]. There are 15 neurons of type, Mi1, in the seven-column dataset of which only seven — Mi1-H (center column) and Mi1-{A-F} (adjoining six column) — are relevant. The remaining eight are likely only partially reconstructed. Aside from the skeleton files — found in ./code/github/FlyConnectome/skeletons/, the primary sources of data in the ./code/github/FlyConnectome/ respository consist of two json files containing Python dict structures:

• neuronsinfo.json — everything you need to know about 462 fully-traced neurons and over 5,000 partially-traced neurons;

• synapses.json — everything you need to know about 53,383 synapses organized in small cohorts called T-bar structures;

References

[1]	A. Bahl, E. Serbe, M. Meier, G. Ammer, and A. Borst. Neural Mechanisms for Drosophila Contrast Vision. Neuron, 88(6):1240--1252, 2015.
[2]	Rudy Behnia, Damon A. Clark, Adam G. Carter, Thomas R. Clandinin, and Claude Desplan. Processing properties of ON and OFF pathways for drosophila motion detection. Nature, 2014.
[3]	Alexander Borst. Fly visual course control: behaviour, algorithms and circuits. Nature Reviews Neuroscience, 15:590--599.
[4]	Alexander Borst and Thomas Euler. Seeing things in motion: Models, circuits, and mechanisms. Neuron, 71(6):974--994, 2011.
[5]	Alexander Borst and Moritz Helmstaedter. Common circuit design in fly and mammalian motion vision. Nature Neuroscience, 18:1067--1076, 2015.
[6]	A. Carlson. Anti-hebbian learning in a non-linear neural network. Biological Cybernetics, 64:171--176, 1990.
[7]	Samir Chowdhury and Facundo Mé́moli. Persistent path homology of directed networks. CoRR, arXiv:1701.00565, 2017.
[8]	T. Erclik, X. Li, M. Courgeon, C. Bertet, Z. Chen, R. Baumert, J. Ng, C. Koo, U. Arain, R. Behnia, A. del Valle Rodriguez, L. Senderowicz, N. Negre, K. P. White, and C. Desplan. Integration of temporal and spatial patterning generates neural diversity. Nature, 541(7637):365--370, 2017.
[9]	P. Földiák. Forming sparse representations by local anti-hebbian learning. Biological Cybernetics, 64:165--170, 1990.
[10]	P. Földiák. Learning invariance from transformation sequences. Neural Computation, 3:194--200, 1991.
[11]	M. Joesch, B. Schnell, S. V. Raghu, D. F. Reiff, and A. Borst. ON and OFF pathways in Drosophila motion vision. Nature, 468(7321):300--304, 2010.
[12]	M. S. Maisak, J. Haag, G. Ammer, E. Serbe, M. Meier, A. Leonhardt, T. Schilling, A. Bahl, G. M. Rubin, A. Nern, B. J. Dickson, D. F. Reiff, E. Hopp, and A. Borst. A directional tuning map of Drosophila elementary motion detectors. Nature, 500:212--216, 2013.
[13]	Alex S. Mauss, Katarina Pankova, Alexander Arenz, Aljoscha Nern, Gerald M. Rubin, and Alexander Borst. Neural circuit to integrate opposing motions in the visual field. Cell, 162:351--362, 2017.
[14]	J. Morante and C. Desplan. The color-vision circuit in the medulla of Drosophila. Current Biology, 18(8):553--565, 2008.
[15]	Javier Morante and Claude Desplan. Building a projection map for photoreceptor neurons in the drosophila optic lobes. Seminars in Cell & Developmental Biology, 15(1):137--143, 2004.
[16]	Nathalie Nèriec and Claude Desplan. Chapter fourteen - from the eye to the brain: Development of the drosophila visual system. In Paul M. Wassarman, editor, Essays on Developmental Biology, Part A, volume 116 of Current Topics in Developmental Biology, pages 247--271. Academic Press, 2016.
[17]	Stephen M. Plaza, Toufiq Parag, Gary B. Huang, Donald J. Olbris, Mathew A. Saunders, and Patricia K. Rivlin. Annotating synapses in large EM datasets. CoRR, arXiv:1409.1801, 2014.
[18]	Dierk F. Reiff, Johannes Plett, Marco Mank, Oliver Griesbeck, and Alexander Borst. Visualizing retinotopic half-wave rectified input to the motion detection circuitry of drosophila. Nature Neuroscience, 13:973--978, 2010.
[19]	Sebastian Seung and Jonathan Zung. A correlation game for unsupervised learning yields computational interpretations of hebbian excitation, anti-hebbian inhibition, and synapse elimination. CoRR, arXiv:1704.00646, 2017.
[20]	Christian Spalthoff, Ralf Gerdes, and Rafael Kurtz. Neuronal representation of visual motion and orientation in the fly medulla. Frontiers in Neural Circuits, 72, 2012.
[21]	S. Y. Takemura, C. S. Xu, Z. Lu, P. K. Rivlin, T. Parag, D. J. Olbris, S. Plaza, T. Zhao, W. T. Katz, L. Umayam, C. Weaver, H. F. Hess, J. A. Horne, J. Nunez-Iglesias, R. Aniceto, L. A. Chang, S. Lauchie, A. Nasca, O. Ogundeyi, C. Sigmund, S. Takemura, J. Tran, C. Langille, K. Le Lacheur, S. McLin, A. Shinomiya, D. B. Chklovskii, I. A. Meinertzhagen, and L. K. Scheffer. Synaptic circuits and their variations within different columns in the visual system of Drosophila. Proceedings of the National Academy of Science, 112(44):13711--13716, 2015.