PSET2, Part 2: Proof Writing

👈 Back to problem set index.

Problem Eight: Yablo's Paradox

A logical paradox is a statement that isn’t true and isn’t false. One of the simplest paradoxes is the Liar's paradox, which is the following:

$(P)$: Statement $(P)$ is false.

If statement $(P)$ is true, then by its own admission statement $(P)$ is false – a contradiction! That means that statement $(P)$ isn't true.

On the other hand, suppose that statement $(P)$ is false. Then we know that “statement $(P)$ is false” is false, meaning that statement $(P)$ is true – a contradiction! This means that statement $(P)$ isn't false either.

Since statement $(P)$ isn't true and isn't false, it's a paradox.

Paradoxes often arise as a result of self-reference. In the Liar's Paradox, the paradox arises because the statement directly refers to itself. However, it's not the only paradox that can arise from self-reference. This problem explores a beautiful, subtle paradox called Yablo's paradox.

Consider the following collection of infinitely many statements numbered $S_0, S_1, S_2, \dots$, where there is a statement $S_n$ for each natural number $n$. These statements are ordered in a list as follows:

  • $(S_0)$: All statements in this list after this one are false.
  • $(S_1)$: All statements in this list after this one are false.
  • $(S_2)$: All statements in this list after this one are false.
  • $\dots$

More generally, for each $n \in \mathbb{N}$, the statement $(S_n)$ is

$(S_n)$: All statements in this list after this one are false.

Surprisingly, the interplay between these statements makes every statement in the list a paradox.

  1. Prove, by contradiction, that there does not exist a natural number $n$ where statement $(S_n)$ is true.

    Something to ponder: how do you negate a universally-quantified statement?

  1. Prove, by contradiction, that there does not exist a natural number $n$ where statement $(S_n)$ is false.

Your results from parts (i) and (ii) collectively establish that every statement in the list above is paradox, since none of them are true and none of them are false.

Now, consider the following modification to this list. Instead of infinitely many statements, suppose that there are “only” $10,000,000,000$ statements. Specifically, suppose we have these statements:

  • $(T_0)$: All statements in this list after this one are false.
  • $(T_1)$: All statements in this list after this one are false.
  • $(T_2)$: All statements in this list after this one are false.
  • $\dots$
  • $(T_{9,999,999,999})$: All statements in this list after this one are false.

There's still a lot of statements here, but not infinitely many of them. Interestingly, these statements are all perfectly consistent with one another and do not result in any paradoxes.

  1. For each statement in the above list, determine whether it's true or false and explain why your choices are consistent with one another.

Going forward, don't worry about paradoxes in CS103. We won't talk about any more statements like these. 😃

Problem Nine: Square and Triangular Numbers

A natural number $n$ is called a square number when there exists a natural number $k$ where $n = k^2\text.$ The first few square numbers are $0, 1, 4, 9, 16, 25, \ldots \text.$ Intuitively, the square numbers count the number of squares in a square grid:

A 1x1 grid with one square, a 2x2 grid with four squares, a 3x3 grid with nine squares, a 4x4 grid with sixteen squares, and a 5x5 grid with twenty-five squares.

A natural number $n$ is called a triangular number when there exists a natural number $k$ where $n = \frac{k(k+1)}{2}\text.$ The first few triangular numbers are $0, 1, 3, 6, 10, 15, \ldots \text.$ Intuitively, the triangular numbers count the number of squares in these figures:

A figure made of a single square, which has one square in it. Next to it is a figure of squares made of two rows of squares. The top row has one square in it. The bottom row has two squares in it. Collectively, the figure has three squares. Next to this is a figure made of three rows of squares. The top row has one square in it. The second row has two squares in it. The third row has three squares in it. Colletively the figure has six squares in it. Next to that is a figure made of four rows of squares. The first row has one square in it. The second row has two squares in it. The third row has three squares in it. The fourth row has four squares in it. Collectively the figure has ten squares.

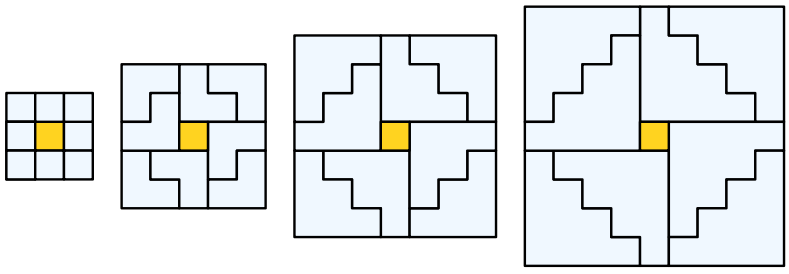
Prove for all natural numbers $n$ that $n$ is a triangular number if and only if $8n + 1$ is a square number. There's a lovely geometric intuition for this shown here:

A 3x3 grid that is covered as follows. There are eight copies of the 1x1 triangular figure around the border, and the middle square is left uncovered. Next to that is a 5x5 grid. It is covered by four 3x2 figures, each of which is broken apart into two copies of the triangular figure with two rows. They are arranged in a pinwheel around the center square, which is left uncovered. Similarly, a 7x7 grid is tiled with four 3x4 rectangles in a pinwheel, leaving the center square uncovered, and the center square is left uncovered.

Just to make sure you didn't miss it, the statement to prove is a biconditional rather than a standard implication.

You may want to make use of a result we proved in lecture.

Problem Ten: Tournament Champions

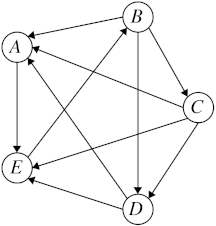
A tournament is a contest among $n \ge 0$ players. Each player plays exactly one game against each other player, and either wins or loses the game (let's assume that there are no draws). We can visually represent a tournament by drawing a circle for each player and adding arrows between pairs of players to indicate who won each game. For example, consider this tournament:

A tournament of five players named A, B, C, D, and E. Player A won against player E and lost to players B, C, and D. Player B won against players A, C, and D and lost to player E. Player C won against players A, D, and E and lost against player B. Player D won against players A and E and lost against players B and C. Player E won against player B and lost against players A, C, and D

In this tournament, player $A$ beat player $E$, but lost to players $B$, $C$, and $D$.

Now, a new definition. A tournament champion is a player $c$ where, for each player $p$ that $c$ lost to, there is a player $q$ where $c$ won against $q$ and $q$ won against $p$.

In the tournament shown above, player $B$ is a champion: she won against $A$, $C$, and $D$, and although she lost to $E$, she won against $D$, who in turn won against $E$. Player $C$ is also a champion: she won against $A$, $D$, and $E$, and the one player she lost to ($B$) is covered because $C$ won against $E$, who in turn won against $B$. Player $A$, however, is not a tournament champion. To see this, $A$ didn’t win against $C$, nor is there any player who $A$ won against who in turn won against $C$.

  1. Is player $D$ a tournament champion? How about player $E$? No justification is required.

    You might have an intuition for what a tournament champion is, but to determine the answers to these questions, you’ll have to look back at the definition.

Here’s an amazing fact about tournaments.

  1. Let $T$ be an arbitrary tournament and $c$ be a player in that tournament. Prove the following statement: if $c$ won more games than anyone else in $T$ or is tied for winning the greatest number of games, then $c$ is a tournament champion in $T$.

    Remember that proofwriting heavily involves leveraging definitions. Intuitively, it makes sense that someone who won the most games did the best in a tournament, but that’s not what’s being asked here. Instead, you’re asked to show that if someone won the most games (or tied for winning the most games), then they specifically meet the criteria described above that characterize a tournament champion.

    A great question to ponder – what has to happen for someone to not be a tournament champion? Don’t guess based on your intuition; negate the definition of a tournament champion and see what happens. You might want to draw a picture of what happens in this case.

A corollary of the result from (ii) is that every tournament with at least one player has at least one tournament champion – pick someone who won the most games or is tied for winning the most games.

The result you proved in part (ii) of this problem is noteworthy for several reasons. First, this is a fundamental result about tournaments – many aspects of tournaments can be better understood by looking at its champions. Second, it’s an example of a style of proof called a proof by extreme case. In a proof of that sort, you pick some “extreme” object, usually the biggest or smallest object of some type, then prove that it has some property. Here, you proved that the “winningest” player must be a tournament champion. Keep this idea in mind for the future – you’ll likely get some more mileage out of it!

Tournaments have many applications in computational complexity theory and in the emerging field of computational social choice theory. A former CS103 TA, Michael Kim, studied them extensively when doing his PhD here in computer science!