CME 338: Large-Scale Numerical Optimization
Description
The main algorithms and software for constrained optimization, emphasizing the sparse-matrix methods needed for their implementation. Iterative methods for linear equations and least squares. Interior methods. The simplex method. Basis factorization and updates. The reduced-gradient method, augmented Lagrangian methods, and SQP methods.
3 units, Spring (Michael Saunders), Grading basis ABCD/NP
Prerequisites: Basic numerical linear algebra, including LU and QR factorizations, and an interest in MATLAB, sparse-matrix methods, and gradient-based algorithms for constrained optimization
Homework, etc
There will be 4 or 5 homework assignments and one somewhat more challenging project. MATLAB is used for computational exercises.
Grades will be assessed from the homework (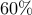 ) and project (
) and project (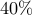 ).
There is no mid-term or final exam.
).
There is no mid-term or final exam.
PLEASE NOTE: The project should be completed by the end of spring quarter. In the past it has been common for work to continue into the summer, but this is not ideal in terms of receiving a grade and pursuing other summer activities.
There is no text book for the class, but see ‘‘references’’ for background reading and a reminder of some of the sources out there. See ‘‘notes’’ for the topics to be covered in turn. Hardcopy of each set of notes will be handed out in class as we progress.
Location
300-380F
Mon Wed 3:00–4:20pm
First class: Mon April 1, 2019
Last class: Wed June 5, 2019
Auditors are welcome
Office hours
Instructor: Prof Saunders, Huang M03 (ICME)
Immediately after class, or most Mon Tue Wed afternoons after 5pm
Course assistants: