Lecture Preview: Dijkstra's Algorithm

(Suggested book reading: Programming Abstractions in C++, Chapter 18 section 18.6)

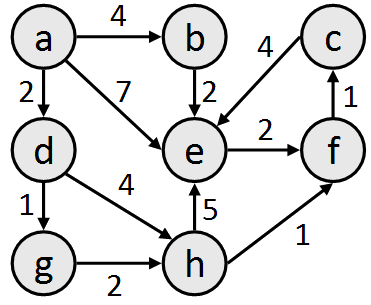
Today we'll learn about an algorithm for searching for paths in graphs, called Dijkstra's algorithm. A breadth-first search (BFS) is guaranteed to find the shortest path between two vertices. (A depth-first search (DFS) is not.) But consider the case of a weighted graph; what if we want to find the path between two vertices that has the lowest total weight? Even a BFS is not guaranteed to find this successfully, because the path with the fewest vertices is not always the lowest-cost path. Consider the graph below, where a BFS from a to f would find the path {a, e, f}, but the path {a, d, g, h, f} has a lower total cost.

dijkstra graph

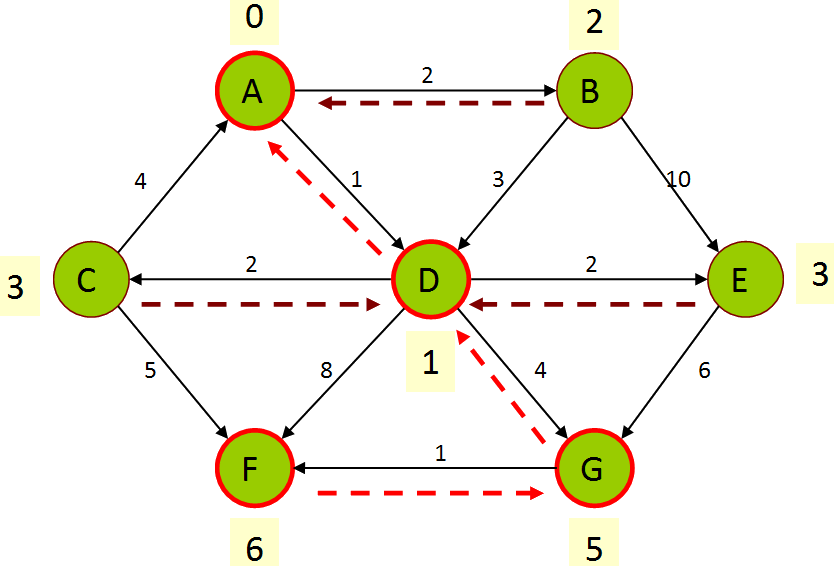
Dijkstra's algorithm is a method of visiting vertices where you always visit the lowest-cost unvisited vertex, then update a set of records of information about the lowest-cost way to reach each vertex so far. You track the total cost by which you could reach the vertex, and the previous vertex you would use to get there. The diagram below of another graph shows an example of the kind of data Dijkstra's algorithm might store when looking for paths from vertex a to f. The path would be {a, d, g, f}, with a total cost of 6.

dijkstra graph 2

This is not a complete description of the algorithm. We will discuss it in detail in lecture, and we will implement it as part of our next homework assignment.

This document and its content are copyright © Marty Stepp, 2018. All rights reserved. Any redistribution, reproduction, transmission, or storage of part or all of the contents in any form is prohibited without the authors' expressed written permission.