CS 106B: Programming Abstractions, Winter 2018

Lecture Preview: Advanced Binary Trees

(Suggested book reading: Programming Abstractions in C++, Chapter 16, sections 16.3 - 16.4)

Today we'll learn about several new varieties of trees. One thing we'll talk about is how to implement a tree map. It is very similar to a tree set, except that our node class stores both a key and a value. For this example, we'll make the keys be strings and the values be integers, though they could be any types you want, so long as the keys can be compared with operators like < and >.

struct TreeMapNode {
    string key;
    int value;
    TreeMapNode* left;
    TreeMapNode* right;
    ...
};

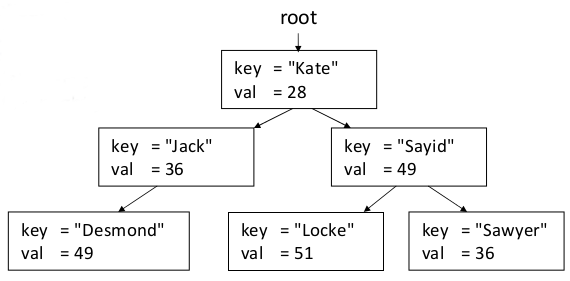
Most of the tree set methods map 1-to-1 to tree map methods. The set's add method is a lot like the map's put, except for the issue of replacing an existing key's value. The set's contains method is a lot like the map's containsKey and get. The set's remove method is a lot like the map's remove.

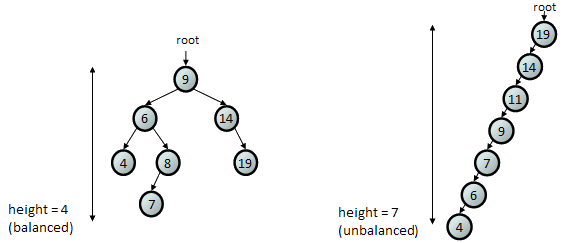
We'll also talk about subspecies of BSTs in the category of balanced binary search trees. Trees that are balanced have a wide appearance and a similar amount of nodes on the left and right, as in the left diagram below. Unbalanced trees tend to be tall and long, with significantly more nodes on one side than the other, as in the right diagram below. Today we will talk about how some variations of trees add measures to ensure that they will always remain balanced. Balance is important for binary search trees to ensure that their runtime for common operations will be O(log N) rather than close to O(N).

Then we'll look some trees that aren't binary search trees, and in some cases aren't even binary trees. One of these is the "prefix tree" or "trie". After tries, I'll introduce your next homework assignment, Huffman encoding trees, and give you a walkthrough of the algorithms you'll need to complete the assignment.