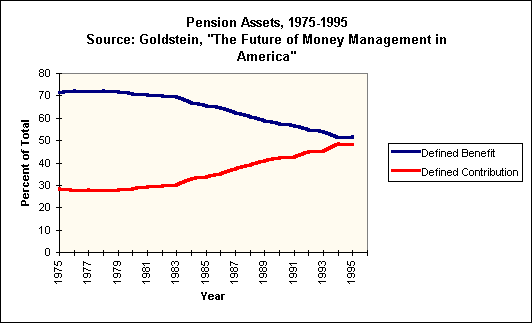
There is a world-wide trend away from defined benefit pension plans, in which workers make no decisions about savings and investment, to defined contribution plans, in which they make such decisions. For example, twenty years ago, 70% of U.S. corporate retirement assets were in defined benefit plans; the proportion is now 50% and falling, as the following figure shows..
This sea change in retirement savings is creating an unprecedented need for ordinary human beings to make informed decisions about investing their retirement savings -- a task for which most are currently ill-equipped. Most participants in defined contribution plans don't know what they are doing and desperately need help.
Since such help must be provided at low cost, we are seeing a plethora of computer-based procedures for such "financial planning". One assumes that the approaches typically implemented in such software reflect the traditional practice of human financial planners, but of course it is difficult to know what goes on between two consenting adults when a financial planner meets a client in the privacy of the planner's office.
I have been studying software provided by major mutual fund and software companies and have found that it reflects remarkably few of the lessons learned after decades of the development of financial theory and its implementation by and for large institutional investors.
Participants in defined contribution plans need economic science, but what they are getting at present is bookkeeping and pseudo-science.
Here is an example of the kind of information that drives such analyses.
Current Age 50 Current Savings $ 100,000 Annual Savings (today's $) $ 12,000 Retirement Age 65 Annual Retirement Spending (today's $) $ 70,000 Years in Retirement 20 Investment Return (%) 10.5 % Inflation (%) 3.5 %
In some cases, questions of mortality are left to the user. In others, the age at death is provided by the software, presumably from a mortality table. But it is always a single number. One dies right on schedule. So much for actuarial science.
Note that the investment return is specified by the user, although most software provides some historic perspective as background for the decision. Imagine complaining about a stomach ache only to have the doctor respond: "Well, do you think it is indigestion, an ulcer or cancer?". If there is an investment expert lurking behind the software, it is one reluctant to give opinions.
Also note that the investment return is summarized with one number. So much for Markowitz's notion of risk.
The implications of these inputs are shown in a graph of one's savings account, produced in living color by virtually all the software packages. Here is an example:
Prior to retirement the account grows regularly, due to new contributions and the unvarying rate of return on assets. After retirement the account eventually begins to diminish as spending overtakes the rate of return, which remains resolutely constant.
Eventually one of two things happens. Either you die (right on schedule) with money in the bank or you run out of money before you die. This case above is one of the happier ones. The user has a bit left at death.In such instances, the software will usually issue a message such as:
CONGRATULATIONS
You have a surplus and will meet or exceed your
goal
or:
CONGRATULATIONS
Your plan works
or the like.
Such messages are usually delivered in green to indicate that everything is a go.
In many cases, however, the situation may be ugly. Here is a case in point:
This poor soul will run out of money before the appointed date with the grim reaper. The software will issue a message such as:
YOU HAVE A SHORTFALL
or:
WARNING
Your plan does not work
Such messages are usually delivered in red, indicating the need to stop and reconsider.
When there is a shortfall, the software packages will generally suggest changes in one or more of four key inputs. To improve the situation, the user is urged to:
The first three choices are, of course, rather painful. But the last one seems easy. Why not choose investments with a higher rate of return? That will clearly improve things. And the software makes it easy to determine the magnitude of the improvement.
What we have here is a return/return tradeoff, rather than the risk/return tradeoff that our textbooks describe. So much for portfolio theory.
To be fair, the software will probably point out that higher returning investments may bring higher "short-term risk". But there is no sign of this in the savings graph. Moreover, such risk has no effect on the deliverance or withholding of congratulations. One is left with the impression that a high-risk investment may go down every so often, but that it will kindly go up subsequently by a large enough amount to get the account back on its appointed track -- mean-reversion with a vengeance.
Of course, one must eventually invest in order to achieve return, and the software packages generally provide advice on this front, although it is sometimes limited to allocation among major asset classes. Here are two examples:
Diagrams of this sort are rather like dinner plates, with the sections indicating proportions of three major food groups. Typically, 6 to 10 such standard menus are offered. At one end is the all-cash, or granola diet, which provides small pleasure but is unlikely to cause much in the way of gastric distress. At the other end is the all-stock, or classic French diet, which will taste delicious but may cause a heart attack or two. While the pain (risk) is sometimes indicated only the pleasure (return) affects the savings account projections.
One might imagine that asset allocations suggested in such software packages conform to the prescriptions of Markowitz, representing points along an efficient risk/return frontier, with each one optimal for a different degree of risk tolerance. However, this seems unlikely. In this case the "moderate" portfolio has 20% in cash and equal parts of bonds and stocks. This would suggest that a 50/50 bond/stock portfolio has the greatest excess return Sharpe ratio. But if this is the case, why is the "conservative" portfolio not a combination with equal parts of bonds and stocks and more cash rather than a mix with the same amount of cash and three times as much in bonds as in stocks.
Here is another example:
As one goes from the "aggressive" to the "moderate" and on to the "conservative" portfolio, the amount invested in stocks declines and the amount invested in cash increases. So far so good. But note what happens to the bond portion. It increases, then decreases. Markowitz showed that in regions of the efficient frontier for which a given set of constraints is binding, every portfolio can be constructed using a linear combination of any other two. Here, there is no way that the moderate portfolio can be constructed by allocating funds between the aggressive and conservative portfolios. The principles that guided the dietitians constructing these menus were not the ones typically taught in business schools.
However important asset allocation may be, ultimately the investor must select specific mutual funds. For this task, software packages tend to either leave the user in a sea of thousands of funds or provide a crude taxonomy involving a few broad categories (such a "growth and income") with all funds in a given category considered equivalent. The latter approach flies in the face of numerous studies that have found the standard fund classifications to be inaccurate in almost every case and intentionally misleading in some.
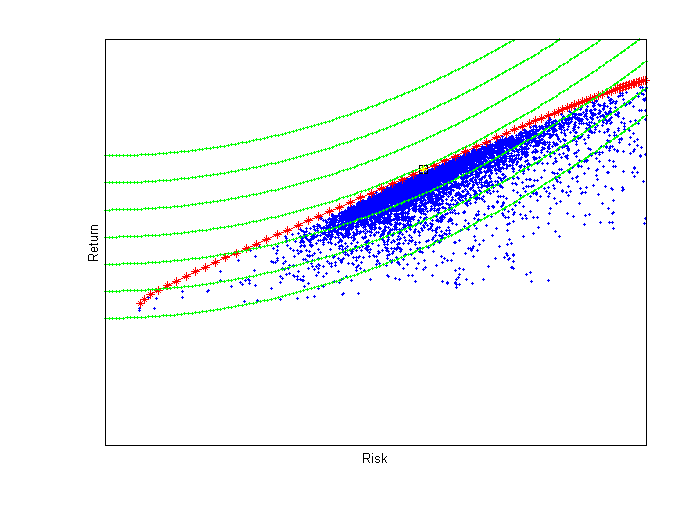
At this point it is useful to recount the key ingredients of portfolio theory. In the diagram below, each point in blue plots the risk and expected return for a specific portfolio composed in a more or less traditional way from 1 to 18 different asset classes. The points in red represent portfolios that are efficient in the sense of Markowitz. Collectively, they form the efficient frontier of risk/return opportunities. For any given level of risk, the efficient portfolio is the one with the greatest expected return.
Estimation of the risk and return of a portfolio and determination of the set of efficient portfolios requires knowledge of financial markets and hence is properly the task of an expert investment advisor.
The curves in green in the diagram represent the attitudes of a particular investor towards risk and return. This investor considers all points on a given green curve to be equally desirable -- that is, he or she is indifferent among them. Points on higher curves are preferred to points on lower curves. There are, of course, many such indifference curves, only a few of which have been shown. Note that the curves slope upward, indicating that the investor will only be willing to take on more risk if there is the prospect for greater expected return. The shape of the curves reflects the investor's degree of tolerance for risk.
Ultimately, only the investor knows his or her risk tolerance.
The goal, of course, is to find the portfolio that will be best for the investor in question. Formally, this lies at the point on the efficient frontier at which one of the investor's indifference curves just touches the frontier -- shown by the yellow point in the figure. To determine this, the information known to the investment advisor must be brought together with the information known to the investor.
There are two ways to do this.
First, the investment advisor can help the investor understand the implications of each of a number of alternative efficient portfolios, letting the investor choose among them. This is almost universally done in institutional investment practice. However, to do this the investment advisor must admit that there is risk and help the investor understand the implications of both risk and return.
Since the typical software package fails to quantify the efficient investment opportunity set in meaningful risk and return terms, a different other approach is taken. The investor is asked a series of questions that attempt to elicit information about his or her preferences (the green curves in the figure). Then the software suggests a portfolio that seems appropriate. Unfortunately, such questions often leave a great deal to be desired. Two types of questions recur.First there are those that try to assess the respondent's willingness to take risk in other contexts -- for example: "Do you like to jump out of airplanes?". The presumption is that those who answer in the affirmative are prime candidates for all-stock portfolios. The second type of question probes the respondent's current investment positions -- for example: "True or False: I have a lot of stocks and am comfortable with the risk." Not surprisingly, those who answer such an inquiry in the affirmative are counseled to have a stock-heavy portfolio. There are other types of questions, such as those that ask about short-term needs for cash, and so on. There may or may not be some sort of science behind such procedures but it seems unlikely that the leap from answers to such questions to a recommended portfolio is a sound one.
Enough bashing of software that is, for all its substantive failings, often aesthetically pleasing and fun to use. It is time to address the two obvious questions. First, why this state of affairs? Second, what might be done instead?
I think there are two major reasons for this situation.
First, there is a perfectly well-placed concern that ordinary human beings just can't understand and process uncertainty. It is thought that probability distributions may be fine in the MBA classroom, but not in the factory. At the very least, it will be a challenge to educate large numbers of people to think probabilistically.
Second, there are the ever-present legal and regulatory constraints. Many believe that it is safer to give no advice than to give good advice. Just as the threat of medical malpractice suits may severely constrain even the most dedicated physician, the threat of fiduciary suits may constrain the most dedicated investment advisor, whether operating in person or via software. To take a key example, it should be the case that a plan sponsor is more likely to be sued for providing little advice or overly simplistic advice than for providing realistic projections that take uncertainty into account. If this is not the case, we need to change public policy so that it will be.
Finally, what should be done? Here the answer is reasonably obvious. We need to devise software that recognizes that investment returns are not certain, that conveys risk/return tradeoffs in ways that are relevant and understandable by the user and that projects mutual fund characteristics as carefully as possible. There is ample experience on this front from institutional practice, in particular pension fund asset allocation studies. But such studies typically cost tens to hundreds of thousands of dollars. We need to bring such technology to individuals for a tiny fraction of that cost. A number of people, myself included, believe that with today's technology this is possible. Time will tell.